Arithmetic sequence
An arithmetic sequence is a sequence where each term is found by adding or subtracting the same value from one term to the next. This value that is added or subtracted is called "common sum" or "common difference"
If the common difference is positive, the terms of the sequence will increase in value.
If the common difference is negative, the terms of the sequence will decrease in value.
For example, the following two sequences are examples of arithmetic sequences.
1, 4, 7, 10, 13, 16, 19, .......
70, 62, 54, 48, 40, ...............
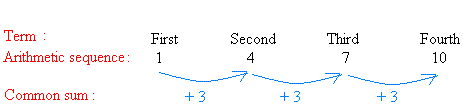
Looking carefully at 1, 4, 7, 10, 13, 16, 19, ......., helps us to make the following observation:
As you can see, each term is found by adding 3, a common sum, to the previous term.

Looking carefully at 70, 62, 54, 46, 38, ......., helps us to make the following observation:
This time, to find each term, we subtract 8, a common difference from the previous term.
Many arithmetic sequences can me modeled with an algebraic expression
Here is a trick or "recipe per se" to quickly get an algebraic expression!
1) Let us try to model 1, 4, 7, 10, 13, 16, 19, .......
Let n represent any term number in the sequence. The number we add to each term is 3.
The number that comes right before 1 in the sequence is -2.
We can therefore model the sequence with this algebra expression: 3 × n + -2.
Check to see if the algebra expression works:
- When n = 1, which represents the first term, we get 3 × 1 + -2 = 3 + -2 = 1
- When n = 2, which represents the second term, we get 3 × 2 + -2 = 6 + -2 = 4
- When n = 3, which represents the third term, we get 3 × 3 + -2 = 9 + -2 = 7
The algebraic expression works!
2) Let us try to model 70, 62, 54, 46, 38, ...............
Let n represent any term number in the sequence. The number we subtract to each term is -8.
The number that comes right before 70 in the sequence is 78.
We can therefore model the sequence with this algebraic expression: -8 × n + 78.
Check to see if the algebra expression works:
- When n = 1, which represents the first term, we get -8 × 1 + 78 = -8 + 78 = 70
- When n = 2, which represents the second term, we get -8 × 2 + 78 = -16 + 78 = 62
- When n = 3, which represents the second term, we get -8 × 3 + 78 = -24 + 78 = 54
Again, the algebraic expression works!
Arithmetic sequence formula
The way that we modeled the arithmetic sequences above with algebraic expressions is a shortcut. We will now look for the arithmetic sequence formula using the algebraic expressions.
1)
3 × n + -2 is the algebraic expression for 1, 4, 7, 10, 13, 16, 19, .......
Let us try to rewrite 3 × n + -2 by making the first term appear in the expression.
3 × n + -2 = 3 × n + -3 + 1 (since -2 = -3 + 1)
3 × n + -2 = 3 × (n - 1) + 1
3 is the number we add to each term
1 is the first term
n is the number of terms
2)
-8 × n + 78 is the algebraic expression for 70, 62, 54, 46, 38, ...............
Let us try to rewrite -8 × n + 78 by making the first term appear in the expression.
-8 × n + 78 = -8 × n + 8 + 70 (since 78 = 8 + 70)
-8 × n + 78 = -8 × (n - 1) + 70
-8 is the number we add to each term
70 is the first term
n is the number of terms
In general,
Let d be the number we add each time or the common difference.
Let a1 be the first term
Let n be the number of terms
Let an be the nth term.
Then, an = d × (n - 1) + a1
A couple of exercises about arithmetic sequences
Are the given sequences arithmetic? If so, find the 98th term.
a. 2, 6, 9, 11, ....
b. -4, 0, 4, 8, 12, ....
2, 6, 9, 11, .... is not an arithmetic sequence since the number we add to each term is not always the same.
-4, 0, 4, 8, 12, .... is an arithmetic sequence since the number we add to each term is always the same.
an = d × (n - 1) + a1
d = 4
n = 98
a1 = -4
a98 = 4 × (98 - 1) + a1
a98 = 4 × (97) + -4
a98 = 388 + -4
a98 = 384