Sequences and patterns

Sequences and patterns arise naturally in many real life situations. Looking at the figure below, could you identify the pattern and continue the sequence?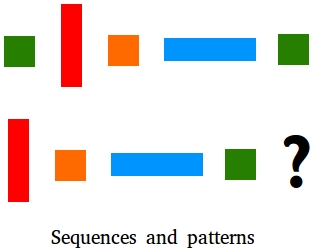

You probably had no difficulties identifying the next shape as the red rectangle. 

Here is though a more stunning, interesting and real-life example of sequences and patterns to introduce the topic.

Say for instance you go to the bank to deposit money and the bank gives you the following two options to choose from:

Option A:

Deposit 1000 dollars.

The second day you receive 1100

The third day you receive 1200

The fourth day your receive 1300

And so forth....

Option B:

Deposit 1 dollar.

The second day you receive 3

The third day you receive 9

The fourth day your receive 27

And so forth....

Which option gives you more money in 10 days?

At first, the tendency is say that option A is the best option.

However, let us take a look and see what is going on here.

If you choose option A,

The fifth day you receive 1400

The sixth day you receive 1500

The seventh day your receive 1600

The eighth day you receive 1700

The ninth day you receive 1800

The tenth day your receive 1900

On the other hand, if you choose option B,

The fifth day you receive 81

The sixth day you receive 243

The seventh day your receive 729

The eighth day you receive 2187

The ninth day you receive 6561

The tenth day your receive 19683

No doubt now you can see clearly that option B is the best option.

Notice that in option A, to get to the next number, just add 100 every time.

We call this pattern an arithmetic sequence. To learn more about this type of sequence, go to arithmetic sequence.

In option B, to get to the next number, just multiply by 3 every time.

We call this pattern a geometric sequence. To learn more about this type of sequence, go to geometric sequence.

The reason the money grew so fast in option B is because the pattern is an exponential growth, which usually grows fast.

The exponential growth above can be modeled with an exponential function.

The exponential function is 3ⁿ

when n = 1, 3¹= 3

when n = 2, 3²= 9

And so forth....