Law of sines

The law of sines, also called sine rule or sine formula, is a very useful trigonometric formula that will help you solve a triangle or find missing measures in a triangle when you know the measures of two angles and a side, or two sides and a nonincluded angle.

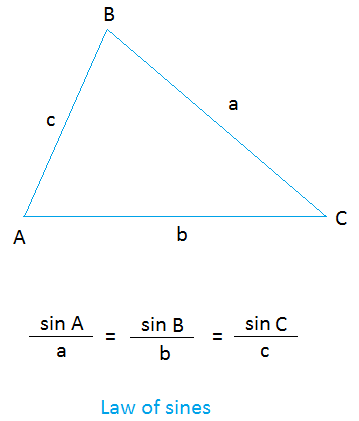
Looking closely at the triangle above, did you make the following important observations?

Side a is opposite to angle A. Side b is opposite to angle B. Side c is opposite to angle C.

Now, how do we know the formula will work?

Now, do this useful experiment below that will really help you understand the sine rule. You will need a piece of paper, a pencil, a protractor, and a scientific calculator.

1. Draw a scalene triangle on a sheet of paper and label the triangle as the one I did above.

2. Use a ruler to measure sides a, b, and c.

3. Use a protractor to measure angle A, angle B, and angle C.

4. Use the sine rule to verify that it works.

I did the same thing for the triangle I drew above and I have found the following measurements.

a = 13 cm , b = 13.7 cm, and c = 9.3 cm

A = 66 degrees, B = 75 degrees, and C = 42 degrees

As you can see, the answers are almost the same. If our measurements were perfect, they will be exactly the same.

In which cases can we use the law of sines?

The different combinations that you can have are

• Only sides: SSS

• Only angles: AAA

• Two sides and one angle: SSA, SAS, and ASS (SSA is the same as ASS)

• Two angles and one side: AAS, ASA, and SAA (AAS is the same as SAA)

Cases when you cannot use the law of sines

Notice that you cannot use the law of sines in the following two cases. You should instead use the law of cosines.

Two sides and the angle between these two sides are known (SAS). 

All three sides of a triangle are known (SSS). 

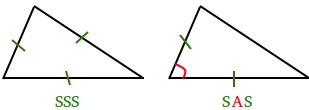
SSS (side-side-side) will not work since you do not know the opposite angle.

SAS (side-angle-side) will not work since you do not know the side opposite the angle.

Cases when you can use the law of sines

You can use the law of sines in the following three cases.

Two sides and the angle opposite to one side are known (SSA or ASS). 

Two angles and the side between these two angles (included side) are known (ASA). 

Two angles and the non-included side are known (AAS or SAA). 

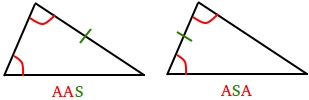
AAS (angle-angle-side) will work as you try to solve the triangle since you can find the last angle or the third angle by using the two angles that are known.

ASA (angle-side-angle) will also work when solving the triangle. However, you must find the unknown angle first before you can use the law of sines.

SSA or ASS is the ambiguous case and it requires a lesson on its own. Please read the lesson about ambiguous case of the law of sines to fully understand it. 

A case when you cannot use either the law of sines or the law of cosines

If all three angles of a triangle are known, but you do not know anything about its sides, then you can neither use the law of sines nor the law of cosines to solve the triangle. 

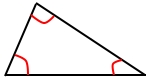
Since you do not know the length of any side, there is nowhere to go from them.

How to use the law of sines to solve a problem when the measures of two angles and a side are given

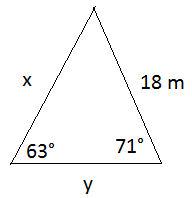
Use the triangle above and the law of sines to find the length of x and the length of y.

Multiply both sides by x

x × 0.0495 = sin(71°)

Divide both sides by 0.0495


Before we can find y, we need to know the measure of the angle that is opposite to y. Call this angle n.

Since the sum of the angle in a triangle is 180°,  63 + 71 + n = 180

134 + n = 180, so  n = 46°

Multiply both sides by y

y × 0.0495 = sin(46°)

Divide both sides by 0.0495