Great law of sines problems

These law of sines problems below will show you how to use the law of sines to solve some real life problems. You will need to use the sine formula shown below to solve these problems.

Law of sines problems

Solving an angle-side-angle (ASA) triangle with the law of sines

Problem #1

Two fire-lookout stations are 15 miles apart, with station A directly east of station B. Both stations spot a fire. The angular direction of the fire from station B is N52°E and the angular direction of the fire from station A is N36°W. How far is the fire from station A? 

Solution

The biggest trick is this problem is to understand the meaning of N52°E and N36°W.

N52°E means 52 degrees east of north.

N36°W means 36 degrees west of north.

Here is what the graph will look like after you draw it.

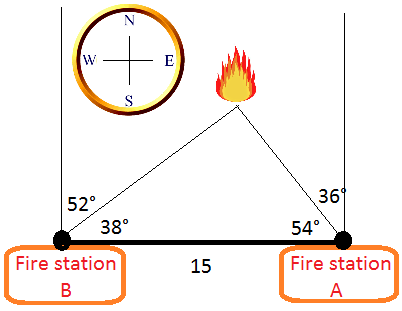
Notice that to find 38°, you need to subtract 52° from 90°. By the same token, to find 54°, you need to subtract 36° from 90°.

Notice also that the angle opposite 15 is missing, so we need to find it.

38 + 54 + missing angle = 180

92 + missing angle = 180, so missing angle  = 88

Now, we can use the sine rule to find the distance the fire is from station A.

Let x be the distance from the fire to station A.

The distance the fire is from station A is = 9.328 miles

Solving an angle-angle-side (AAS) triangle with the law of sines

Problem #2

The leaning tower of pisa is inclined 5.5 degrees from the vertical. At a distance of 100 meters from the wall of the tower, the angle of elevation to the top is 30.5 degrees. Use the law of sines to estimate the height of the leaning tower (height as shown in the image below with the green line) 

Solution

The trickiest thing here is making the graph. We show it below. Notice that the height is shown with a green line.

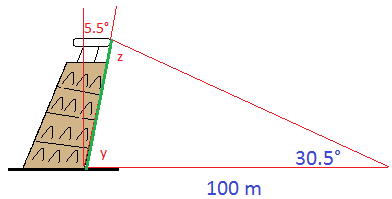
Let us find angle y and angle z

angle y + 5.5 = 90, so angle y = 84.5

84.5 + 30.5 + angle z =180

115 + angle z = 180

angle z =  65

Now, we can use law of sines.

Height of tower = 56 meters

In reality, the height of the leaning tower of pisa is 55.86 meters

Solving a side-side-angle (SSA) triangle with the ambiguous case of the law of sines

Problem #3

A homeowner is trying to build a raised garden bed that has a triangular shape. His neighbor gave him two pieces of lumber with lengths 20 feet and 8 feet and he puts them together to begin his triangle. He is planning to go to the store to buy the third piece of lumber to finish the triangle. He wants to build the triangular garden so that third piece of lumber will make an angle of 40 degrees with the piece that is 20 feet long. Will it be possible for him to make the garden? If so, how long should the third piece of lumber be?

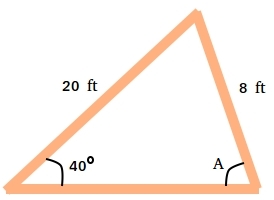
If the homeowner could build such a garden, it will look like the figure shown above. An angle A would then be formed between the third piece of lumber and the piece that is 8 feet long.

Let us use the law of sines to see if this is possible.

sin (40 degrees) / 8 = sin (A) / 20

0.642 / 8 = sin (A) / 20

0.08025 = sin (A) / 20

Multiply both sides of the equation by 20

0.08025(20) = [sin (A) / 20](20)

0.08025(20) = sin (A) 

0.08025(20) = sin (A) 

1.605 = sin(A)

The sine of an angle must be smaller than 1. Since Angle A cannot be formed, it will not be possible to make such a garden. Since the angle cannot be formed, the piece that is 8 feet long will never meet with the third piece. As a result, he will never know the length of the third piece. 

If the homeowner knows how to use the ambiguous case of law of sines, then he will do that first before driving to the store!