Ambiguous case of the law of sines

The ambiguous case of the law of sines happens when two sides and an angle opposite one of the two sides are given. We can shorten this situation with SSA.

Since the length of the third side is not known, we don't know if a triangle will be formed or not. That is the reason we call this case ambiguous.

In fact, this kind of situation or SSA can give the following 4 scenarios.

  • No triangle
  • 1 triangle
  • 1 right triangle
  • 2 triangles

The first scenario of the ambiguous case of the law of sines occurs when a < h.

For example, take a look at the triangle below where only two sides are given. These two given sides are a and b. An angle opposite to one side is also given. Angle A is the angle that is opposite to side a or one of the two sides.

Note that SSA in this case means side a side b angle A in that order.

Ambiguous case of the law of sines when no triangle can be formed

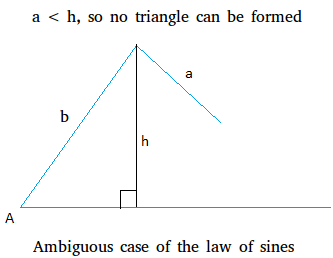
Because a is shorter than h, a is not long enough to form a triangle. In fact, the number of possible triangles that can be formed in the SSA case depends on the length of the altitude or h.

Notice that sin A =
h / b

Once you multiply both sides of the equation above by b, we get h = b sin A.

An example showing that no triangle can be formed 

Method #1

Suppose A = 74°, a = 51, and b = 72.

h = 72 × sin (74°) = 72 × 0.9612 = 68.20

Since 51 or a is less than h or 69.20, no triangle will be formed.

Method #2

We can also show that no triangle exists by using the law of sines.

a / sin A = b / sin B

The ratio a / sin A is known since a / sin A = 51 / sin 74°

Since we also know the length of b, the missing quantity in the law of sines is sin B. It is logical then to look for sin B and see what we end up with.

51 / sin 74° = 72 / sin B

51 sin B = 72 sin 74°

sin B = (72 sin 74°) / 51

sin B = (72 × 0.9612) / 51

sin B = (69.2064) / 51

sin B = 1.3569

Since the sine of an angle cannot be bigger than 1, angle B does not exist. Therefore, no triangle can be formed with the given measurements.

The second scenario of the ambiguous case of the law of sines occurs when a = h.

When a = h, the resulting triangle will always be a right triangle.

Ambiguous case of the law of sines when one right triangle can be formed

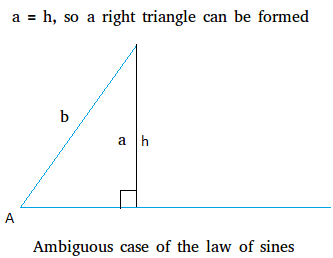
An example showing that a right triangle can be formed 

Method #1

Suppose A = 30°, a = 25, and b = 50.

h = 50 × sin (30°) = 50 × 0.5 = 25

Since 25 or a is equal to h or 25, 1 right triangle will be formed.

Method #2

Again, we can use the law of sines to show that this time sin B exists and it is equal to 90 degrees.

a / sin A = b / sin B

25 / sin 30° = 50 / sin B

25 sin B = 50 sin 30°

sin B = (50 sin 30°) / 25

sin B = (50 × 0.5) / 25

sin B = (25) / 25

sin B = 1

B = sin-1(1) = 90 degrees.

The third scenario of the ambiguous case of the law of sines occurs when a > h and a > b.

When a is bigger than h, again a triangle can be formed. However, since a is bigger than b, we can only have one triangle. Try to make a triangle where a is bigger than b, you will notice that there can only be 1 such triangle.

Ambiguous case of the law of sines when exactly 1 triangle can be formed

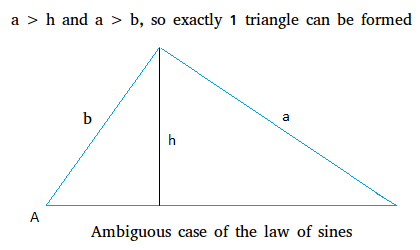
An example showing that exactly 1 triangle can be formed 

Suppose A = 30°, a = 50, and b = 40.

h = 40 × sin (30°) = 40 × 0.5 = 20

Since 50 or a is bigger than both h (or 20) and b (or 40), 1 triangle will be formed.

Last situation:  a > h and a < b

When a is less than b, 2 triangles can be formed as clearly illustrated below. The two triangles are triangle ACD and triangle AED. 

Ambiguous case of the law of sines when 2 triangles can be formed

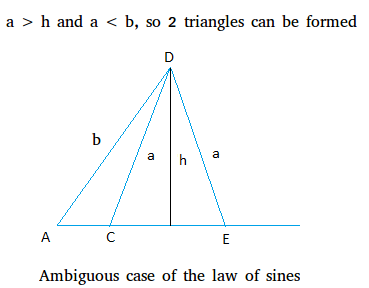
An example showing that exactly 2 triangles can be formed 

Suppose A = 30°, a = 40, and b = 60

h = 60 × sin (30°) = 60 × 0.5 = 30

Since 40 or a is bigger than h and a is smaller than b or 60, 2 triangles will be formed.

Law of sines