Law of Cosines

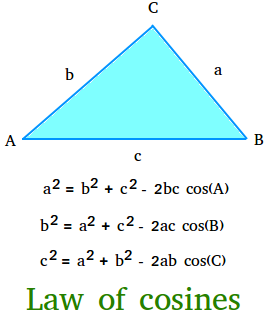
The Law of Cosines, also called Cosine Rule or Cosine Law, states that the square of a side of a triangle is equal to the sum of the squares of the other two sides minus twice their product times the cosine of their included angle.

Law of Cosines formula

When should you use the Law of Cosines?

We use the Law of Cosines to solve an oblique triangle or any triangle that is not a right triangle. When solving an oblique triangle, you are trying to find the lengths of the three sides and the measures of the three angles of the oblique triangle.

Solving an SAS triangle or Side-Angle-Side triangle

If two sides and the included angle (SAS) of an oblique triangle are known, then none of the three ratios in the Law of Sines is known. Therefore you must first use the law of cosines to find the third side or the side opposite the given angle. Follow the three steps below to solve an oblique triangle.

1. Use the Law of Cosines to find the side opposite the given angle
2. Use either the Law of Sines or the Law of Cosines again to find another angle 
3. Find the third angle by subtracting the measure of the given angle and the angle found in step 2 from 180 degrees.

Solving an SSS triangle or Side-Side-Side triangle

If three sides (SSS) are known, solving the triangle means finding the three angles. Follow the following three steps to solve the oblique triangle.

1. Use the law of cosines to find the largest angle opposite the longest side
2. Use either the Law of Sines or the Law of Cosines again to find another angle
3. Find the third angle by subtracting the measure of the angles found in step 1 and step 2 from 180 degrees.

Examples showing how to use the Law of Cosines

Example #1:

Solve the triangle shown below with A = 120 degrees, b = 7, and c = 8.

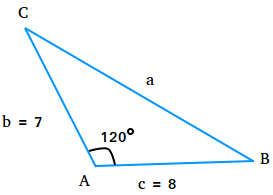
a² = b² + c² - 2bc cos(A)

a² = 7² + 8² - 2(7)(8) cos(120)

a² = 49 + 64 - 2(56)(-0.5)

a² = 113 + 1(56)

a² = 113 + 56

a² = 169

a = √169 = 13

Use the Law of Sines to find angle C

sin C / c =  sin A / a

sin C / 8 =  sin 120 / 13

sin C / 8 =  0.866 / 13

sin C / 8 =  0.0666

Multiply both sides by 8

sin C = 0.0666(8)

sin C = 0.536

C = arcsin(0.5328)

C = 32.19

Angle B = 180 - 120 - 32.19

Angle B = 27.81

The lengths of the sides of the triangle are 7, 8, and 13. The measures of the angles of the triangle are 27.81, 32.19, and 120 degrees.

Example #2:

Solve a triangle ABC if a =  9, b = 12, and c = 10.

There are no missing sides. We just need to find the missing angles. Since the angle opposite the longest side is angle B, use b² = a² + c² - 2ac cos(B) to find cos(B). 

b² = a² + c² - 2ac cos(B)

12² = 9² + 10² - 2(9)(10) cos(B)

144 = 81 + 100 - 2(90) cos(B)

144 = 181 - 180 cos(B)

144 - 181 = -180 cos(B)

-37 = -180 cos(B)

Divide both sides by -180

cos(B) = -37 / -180 = 0.205

B = arccos(0.205)

B = 78.17 degrees

Use the Law of Sines to find angle A

sin(A) / a =  sin(B) / b

sin(A) / 9 =  sin(78.17) / 12

sin(A) / 9 =  0.97876 / 12

sin(A) / 9 =  0.081563

Multiply both sides by 9

sin(A) = 0.081563(9)

sin(A) = 0.734

A = arcsin(0.734)

A = 47.22 degrees

Angle C = 180 - 78.17 - 47.22

Angle C = 54.61

Proof of the Law of Cosines

To prove the Law of Cosines, put a triangle ABC in a rectangular coordinate system as shown in the figure below. Notice that the vertex A is placed at the origin and side c lies along the positive x-axis.

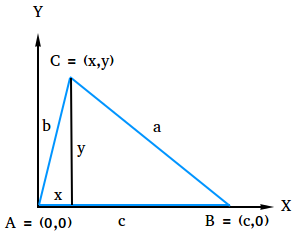
Use the distance formula and the points (x,y) and (c,0) to find the length of a.

a = √[(x - c)² + (y - 0)²]

a = √[(x - c)² + y²]

Square both sides of the equation

a² = (x - c)² + y²

Now, we need to find x and y and replace them in a² = (x - c)² + y²

Using the triangle, write expressions for sin A and cos A and then solve for x and y.

sin(A) = y / b, so y = bsin(A)

cos(A) = x / b, so x = bcos(A)

a² = (bcos A - c)² + (bsin A)²

a² = b² cos² A - 2bc cos A + c² + b² sin² A

Rearrange terms

a² = b² cos² A + b² sin² A + c² - 2bc cos A 

a² = b²(cos² A + sin² A) + c² - 2bc cos A 

a² = b²(1) + c² - 2bc cos A  since cos² A + sin² A = 1

a² = b² + c² - 2bc cos A.