Examples of inductive reasoning

Examples of inductive reasoning are numerous. Lots of IQ or intelligence tests are based on inductive reasoning. Patterns and inductive reasoning are closely related.

Find here a couple of good examples of inductive reasoning that will really help you understand inductive reasoning. But what is inductive reasoning?

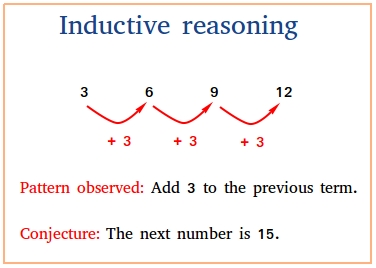
Inductive reasoning is making conclusions based on patterns you observe.The conclusion you reach is called a conjecture.

In the figure below, notice that 3 is added to the previous term in order to get the current term or current number. The logical conclusion we can make based on this pattern is that to find all the numbers after 12, just keep adding 3.

Shapes and inductive reasoning

Example #1:

Look carefully at the following figures. Then, use inductive reasoning to make a conjecture about the next figure in the pattern.


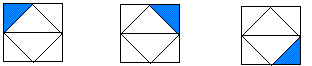If you have carefully observed the pattern, may be you came up with the figure below:

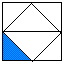Example #2:

Look at the pattern below. Can you draw the next figure or next set of dots using inductive reasoning?

The trick is to see that one dot is always placed between and above two dots. Also, the next figure always has one more dot at the very bottom row.

keeping this in mind, your next figure should look like this:

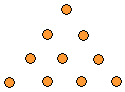Other examples of inductive reasoning: Integers and inductive reasoning

Example #3:

Take a look at this table that shows multiplication as repeated addition:

Multiplication               Repeated addition             Sum

     4 × -2                          -2 + -2 + -2 + -2                   - 8

     3 × -7                               -7 + -7 + -7                     - 21

     5 × -6                         -6 + -6 + -6 + -6 + -6             - 30

What do you notice about the signs of the sums? Since the sum is always negative, the pattern suggests that the product of a positive integer and a negative integer is negative.

Example #4:

Look at the following patterns:

3 × -4 = -12

2 × -4 = -8

1 × -4 = -4

0 × -4 = 0

-1 × -4 = 4

-2 × -4 = 8

-3 × -4 = 12

Every time the factor on the left is decreased by 1, the answer is increased by 4.

However, the pattern suggests that a negative times a negative is a positive.

I hope these examples of inductive reasoning were not complicated.