There is no rational number whose square is 2
In order to prove that there is no rational number whose square is 2, we will use indirect reasoning and we will show that this will lead to a contradiction.
Keep in mind that what we are trying to prove here is that the square root of 2 cannot be a rational number.
In other words, we cannot rewrite the square of 2 so that it will have a numerator and a denominator where the numerator and the denominator are whole numbers.
So, in order to do an indirect proof, we will assume that the square of 2 can be a rational number.
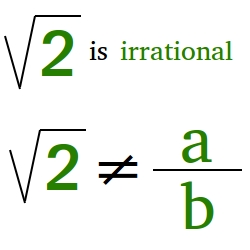
Notice that if we raise both sides of √2 = a/b, we get 2 = (a/b)2
Here is then how to prove that there is no rational number whose square is 2
Indirect reasoning : Suppose that there is a rational number a/b such that
(a/b)2 = 2 (This equation means that 'there is a rational number whose square is 2')
a2/b2 = 2
After multiplying both sides by b2, we get a2 = 2b2
Since a2 = 2b2 they must have the same prime factorization. (Does this make sense? Well, if 10 = 10, then 10 must have the same prime factorization as 10)
Now, we will not prove it, but any number raised to the second power has an even number of prime factors.
(42 = 16 = 2 × 2 × 2 × 2. Then, 16 has 4 prime factors and 4 is an even number)
(82 = 64 = 2 × 2 × 2 × 2 × 2 × 2. Then, 64 has 6 prime factors and 6 is an even number)
b2 will also have an even number of prime factors.
If b2 has an even number of prime factors, 2b2 will have an odd number of prime factors (The 2 next to b2 adds an extra prime factor)
This is a contraction because we said before in blue that they a2 and 2b2 have the same prime factorization. However, now we are saying that they don't in the sentence shown in red.
Therefore, it was wrong for us to assume that the square of 2 can be a rational number.
Conclusion: There is no rational number whose square is 2.