Proof of the Pythagorean Theorem

President Garfield found a proof of the Pythagorean Theorem. Here is how it goes!

Start with two right triangles with legs a and b, and hypotenuse c. Notice that it is the same triangle.


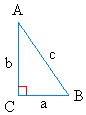Put the two triangles next to each other so that legs a and b form a straight line.

You just have to rotate the triangle on the right 90 degrees counterclockwise. Then move it to the left until it touches the triangle on the left.


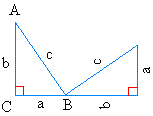
Connect the endpoints to make a trapezoid like the one you see below:



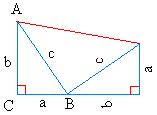
Label the angles inside the triangles as shown below. This will help us prove that the triangle in the middle (one side is red) is a right triangle.



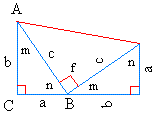
The important thing here to notice is that there are 3 triangles and put together, these triangles form a trapezoid.

Therefore, the area of the 3 triangles must equal the area of the trapezoid.

The area of triangle ABC is (base × height ) / 2

The area of triangle ABC = (a × b ) / 2

The triangle on the right is the same triangle, so the area is also (a × b ) / 2

Now, what about the triangle in the middle or the one with a red side?

Notice that angle m + angle n = 90 degrees. And m + n + f = 180 degrees

90 + f = 180

f = 90 degrees

The triangle in middle is then a right triangle. Thus, the height is also equal to the base or c and area = ( c × c ) / 2 = c² / 2

Area of trapezoid = h/2 × (b₁ + b₂)

Area of trapezoid = ((a + b)/2) × (a + b)

Finally, translate "the area of the 3 triangles must equal the area of the trapezoid" into an equation.

(a × b ) / 2 + (a × b ) / 2 + c² / 2 = ((a + b) / 2) × (a + b)

(a × b + a × b ) / 2 + c² / 2 = ((a + b) / 2) × (a + b)

(2 × a × b) / 2 + c² / 2 = (a + b)² / 2

Multiply everything by 2

2 × a × b + c² = (a + b)²

2 × a × b + c² = a² + 2 × a × b + b²

Subtract 2 × a × b from both sides:

c² = a² + b²

Proof of the Pythagorean Theorem is complete!

A couple of lessons that I recommend before trying to understand the proof of the Pythagorean Theorem.

Pythagorean Theorem

Pythagorean Theorem worksheet