The tangent ratio
This activity is about tangent ratios. Once you complete the activity, the word tangent will make lots of sense to you.
This lesson is the beginning of a series of trigonometric lessons I will provide you with that will help you master trigonometry.
Do the following activity
1. Use a protractor and a ruler to build 3 right triangles of different sizes.
The measure of one of the 3 angles should be 45 degrees.
Your triangles may look like these triangles I made myself.
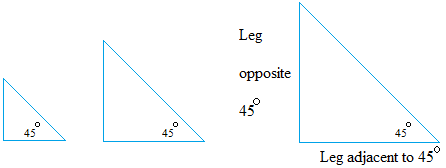
I labeled one of the 3 triangles in order to show the leg that is adjacent to the angle of 45 degrees and the leg that is opposiste to the angle of 45 degrees.
Notice that 45 degrees is just my choice. You could pick any angle you like to do this activity.
2. Measure the legs of all 3 triangles as accurate as possible. (opposite and adjacent legs only!)
For the first triangle on the left, I got 1.6 cm for both opposite and adjacent legs.
For the triangle in the middle, I got 2.7 cm for both opposite and adjacent legs.
For the triangle on the right, I got 3.8 cm for both opposite and adjacent legs.
Notice that the ratio is constant no matter the size of the triangle. If you repeat the activity with an angle of 30 degrees and you made sure that the triangles have different sizes, you will still discover that the ratio is 0.57 for all the triangles no matter the size of the triangles.
This specific ratio, also called trigonometric ratio, is called tangent ratio.
We then say that tangent of 45 degrees is equal to 1. In short, we can use the symbol tan instead of tangent and write tan (45 degrees) = 1
For the angle of 30 degrees, tan (30 degrees) = 0.57
The word tangent may sound fancy to you, yet it is just a ratio. Think of it as a ratio.
There are other ratios such sine and cosine ratios. It makes sense that we use different names to differentiate them. Whenever the ratio involves the opposite side and the adjacent side of an angle, you will call it tangent ratio.
Lesson #2: The sine / cosine ratio