10 cool math tricks

This unit is dedicated to showing you a variety of cool math tricks that can help you tackle some basic math problems with speed and great accuracy. No calculator is needed of course!

Multiplication by 9 using your fingers

Even if you know your multiplication table, this trick may come in handy if you are having a brain freeze all of a sudden. First, put your left hand and your right hand up and starting with your left little finger number your fingers as shown below.

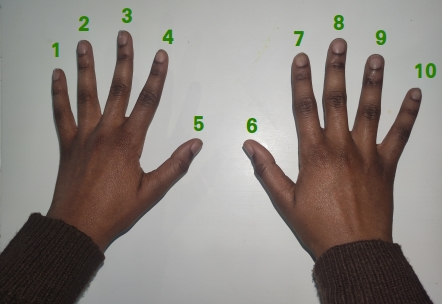
Example #1

To do 9 × 5, fold or lower your fifth finger. The fingers to the left of the lowered finger or fifth finger are the tens and the fingers to the right of the lowered finger are the ones.

There are 4 fingers to the left of the lowered finger and 5 fingers to the right of the lowered finger. So the answer is 45!

Example #2

To do 9 × 6, lower your sixth finger. The fingers to the left of the lowered finger are the tens and the fingers to the right of the lowered finger are the ones.

There are 5 fingers to the left of the lowered finger and 4 fingers to the right of the lowered finger. So the answer is 54!

Two-digit addition

Most of us learn to add on paper from right to left. And it is fine when doing math with paper and pencil. However, if you want to add 2-digit numbers fast in your head, it is better to add from left to right.

Example #3

56
+ 23

A quick way to add 56 and 23 is to follow the 3 easy steps below:

Step 1:

Rewrite 23 as 20 + 3.

Step 2:

Add 56 and 20 since it is easy to add tens. You get 76.

Step 3:

Finally, just add 3 to 76 and the answer is 79.

Example #4

64
+ 35

Step 1:

Rewrite 35 as 30 + 5.

Step 2:

Add 64 and 30 and you get 94

Step 3:

Finally, just add 5 to 94 and the answer is 99

Multiplying any number by 10, 100, 1000, etc...

To multiply a number by 10, just add one zero next to the number.

To multiply a number by 100, just add two zeros next to the number.

To multiply a number by 1000, just add three zeros next to the number.

Example #5

65 × 10 = 650

Example #6

14778 × 1000 = 14778000

Squaring a two-digit number fast

Now, we show you a math trick that you can use to square a number easily and fast. Take a close look at the figure below! It shows how you can use a cool math trick to square a two-digit number much faster than the traditional way of doing it.

The goal is to rewrite one of the numbers being multiplied so that it will have 1 or more zeros.

At this point, there may be one thing that you may not quite understand. Why did we add 4² to 10 × 18? Keep reading as we show you the math behind it!

10 × 18 = (14 - 4)(14 + 4)

10 × 18 = 14 × 14 + 14 × 4 - 14 × 4 - 4²

10 × 18 = 14 × 14 + 56 - 56 - 4²

10 × 18 = 14 × 14 - 4²

Now, all we have to do is to add 4² to both sides of 10 × 18 = 14 × 14 - 4²

10 × 18 + 4² = 14 × 14 - 4² + 4²10 × 18 + 4² = 14 × 14 (Here we go!)

In general,

Let X and c be a natural number. If X + c or X - c gives a number that has 1 or more zeros, then you can multiply X by X easily using the equation X² = (X + c)(X - c) + c²

Example #7

17² = (17 - 7)(17 + 7) + 7²

17² = (10)(24) + 49

17² = 240 + 49

17² = 289

More cool math tricks

Multiplying 6 by an even number less than 10

If you multiply an even number less than 10 by 6, here is how the answer will look like.

The number in the ones place will be the even number you multiply 6 by.

The number in the tens place will be half the even number.

Example #8

6 × 8 = 48

6 × 6 = 36

How to quickly multiply any number by 9

You can quickly multiply any number by 9 by following the following two easy steps:

Step 1: Multiply the number by 10.

Step 2: Subtract the number from the answer you got in step 1.

Example #9

Here is how to multiply 18 by 9.

18 × 10 = 180

180 - 18 = 162

Why does it work?

18 × 9 = 18(10 - 1)

18 × 9 = 18 × 10 - 18 × 1

18 × 9 = 180 - 18

Why do we use it?

Because it is easy to multiply any number by 10

How to quickly subtract numbers

Suppose you are subtracting 28 from 65. Doing vertical subtraction is fine. However, if you are pressed for time and you need to get an answer quick, this is not the time to set up vertical subtraction and then do borrowing and regrouping.

Here is the trick: Subtract 30 from 65 to get 35 and then add 2 since you subtracted 2 more than what you were supposed to. The answer is 37.

Again, we do this because it is kind of easy to subtract tens from any number.

Example #10

461 - 297

461 - 300 = 161

161 + 3 = 164

You would not have found the answer in a snap of a finger had you done vertical subtraction with borrowing and regrouping.

How to square a 2-digit number ending with 1

41²

Subtract 1 from 41 to get 40.

Then add 1 and twice 40 to the square of 40.

40² + 40 + 40 + 1 = 1600 + 80 + 1 = 1681

Example #11

Find 61²

61 = 60² + 60 + 60 + 1 = 3600 + 120 + 1 = 3721

How to quickly test if a number is divisible by another number less or equal to 10

Sometimes you need to quickly find out if you can share something evenly between 2, 3, 4, 5, 6, 7, 8, 9, or 10 people. Then, do not do long division! Just follow these simple divisibility rules.

For example, a number is divisible by 3 if the sum of the digits of the number is divisible by 3.

Example #12

Can you share 4557 dollars evenly between you and your two sisters?

Since 4 + 5 + 5 + 7 = 9 + 12 = 21 and 21 is divisible by 3, then the answer is yes.

How to quickly do division and avoid long division

Divide 4557 by 3.

3 × 1500 = 4500

4557 - 4500 = 57

3 × 19 = 57

4557

Here are a few more interesting and cool math tricks!

Multiplying by powers of ten
Learn to multiply by powers of ten the easy way with these useful shortcuts tricks

Multiplication by 11
Learn how to perform multiplication by 11 in 10 seconds or less with these useful tricks

Squaring numbers ending with five
What if you could square any number two digit number ending in five in 4 seconds or less?

Finger multiplication
Easy, straightforward, and quick multiplication with your fingers!

Number trick with 1089
impress your friends with this 1089 trick!

Compensation
Learn how to use compensation to quickly add, subtract, divide, and multiply

Hopefully, these cool math tricks gave you greater confidence in math. They can be used as magic tricks to impress your friends or as simple shortcuts if you want to do the math in your head.

How to solve some basic math puzzles