SAT math test

• What is the SAT math test? How to ace it
• What are grid-in questions? 
• What topics are tested in the math section of the SAT? 
• How can you prepare effectively for the math section? 
• Tips for doing well on the math test
• Example problems that you should be able to solve - No calculator section
• Example problems that you should be able to solve - Calculator section 

What is the SAT math test? How to ace it

The SAT is a standardized, comprehensive assessment that colleges and other institutions of higher education use to see how much students retained from high school. The test lasts three hours and is usually taken by 11th and 12th graders hoping to gain an edge in the college admission process. 

The SAT math section consists of a calculator section and a non-calculator section. 

The non-calculator section comes first and has 20 total questions: 15 multiple-choice questions and 5 grid-in questions. 25 minutes are given for this section. The calculator section has 38 total questions: 30 multiple-choice questions and 8 grid-in questions. 55 minutes are given for this section. 

What are grid-in questions? 

Grid-in questions are a type of question you will encounter on the SAT math test. These are also known as student-response questions, meaning that it's not a multiple choice question where you have to choose from a set of options. You will need to solve the problem and write your answer in the provided grid-in section on the answer sheet. 

You will receive clear instructions on how to proceed with these questions on the test. If you would like to see an example of how to fill these out, take a look at the grid-in below

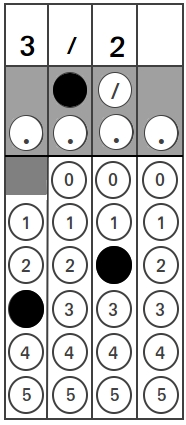
If you solve a problem and the answer you get is 3/2, take a look at the grid-in above to see how to will enter 3/2.

What topics are tested in the math section? 

The College Board, which is the official administrator of the SAT, breaks the SAT math test down into four groups of questions. 

• The first group is called Heart of Algebra. This type of question focuses on functions and linear equations, as well as systems of linear equations. You will encounter 19 of these questions on the test.

• The second group is called Problem Solving and Data Analysis. This section covers ratios and percentages, with the main skill being the ability to apply math to real-world situations. You will encounter 17 of these questions on the test. 

• The third group, Passport to Advanced Math, covers more complex functions and equations. This section aims to prepare students for more advanced subjects, like calculus and statistics. You will encounter 16 of these questions on the test. The last group of questions is Additional Topics in Math, which covers trigonometry, geometry, complex numbers, and radian measure. The test will cover six questions from the additional topics section, three in the non-calculator section and three in the calculator section.

How can you prepare effectively for the SAT math section? 

Your biggest help when preparing for the SAT math test is practice questions and exams. There is an abundance of books, websites, and other helpful sources that have practice tests available for students. 

Try to take a variety of tests, both computer-based and paper-based. The advantage of some computer-based tests is that you may have the possibility to receive feedback on your answers right away. However, one advantage of paper-based practice tests is that you can better mimic real testing conditions. 

When beginning to study, determine which subject areas you are weakest in. For example, if you have trouble with algebra, plan to review algebra-related topics. 

The advantage of taking SAT math practice tests is that they often reflect real question formats. The SAT math is very predictable and foreknowledge of what will be on the test can help you study more effectively. For example, the test is organized from easier to more difficult. This means that the questions will get progressively harder. 

Tips for doing well on the SAT math test

Use the Elimination Method 

You've probably heard that the SAT math test no longer has something called a guessing penalty. Before March 2016, if you guessed incorrectly, you would receive a small penalty. Since that doesn't exist anymore, use the elimination method to your advantage. 

If you've tried to solve the problem but still have no idea what the answer is, you can increase your chances of getting the correct answer by eliminating the answers you know are obviously wrong, and taking your best guess. You won't be penalized for a wrong answer!

Be Careful with the Answer Grid (Multiple Choice Section) 

It might sound simple and obvious, but be careful: The answer grid is unforgiving. 

1. While working through the multiple choice section, you might find the answer and have solved a problem correctly, but you won't get credit if you fill out the wrong bubble on the grid. Make sure that you're filling out the correct bubble for the correct question.

2. Also, keep track of any questions you've skipped. It's very easy to get mixed up and fill in the bubble for a question you've skipped. Let's say for example that you have skipped question 3 in your test booklet. Watch out! Don't fill in the answer for question 4 in the space for question 3. 

Some experienced test takers recommend circling the questions in your answer booklet that you've skipped and then going back and comparing your booklet to your grid afterward. This helps you to consciously skip the question in both places, your test booklet and your answer sheet. 

3. Another tip when taking the SAT math is to wait to mark your answers on the grid. Instead of transferring your answers after every question, wait until you've solved five questions and mark all of them at once. This will help with your concentration and will decrease the chance of making a mistake. 

Bottom line: Always double and triple-check your answer grid with your answers in the booklet. 

Skip Ahead and Move Around 

One common mistake that test takers make is spending too much time on the questions that they find difficult. They work on the question for a long time, wasting precious minutes that could be used to solve two or three other easier questions. 

The solution? If you come across a question that seems difficult, or you find a question where the solution isn't obvious, circle the question and move on to another question that you can solve quickly. Leave the hardest questions for last. 

By the time you come back to the more difficult questions, you may realize that the answer was simpler than you initially thought.  

Use Your Calculator Wisely 

One section of the SAT math test allows you to use a calculator as an aide. However, don't allow the calculator to slow you down. 

Some test-takers make the mistake of pulling out their calculators for every single question during this section. Realistically, there will be some questions that you won't need to use your calculator for. Instead of using it as a crutch, focus on using your prior knowledge about the question to get as far as you can in the solution without the calculator. This will save you time as well. 

You can also use the calculator to double-check your answers. Once you have finished the test, you can use the extra time to go through the test again and double-check your answers using the calculator. 

Manage Your Stress

The best way to manage your stress before taking the SAT math test is to take control of your situation. Once the feeling of helplessness is gone, you'll be better able to see what you need to focus on during your studying. 

The important thing is to have concrete things to do. Make a list of your strengths and weaknesses, and then create a schedule to work on each of the topics. 

Another strategy is to use relaxation exercises when you find yourself too stressed to concentrate. Below are some recommended exercises. 

1. Try to visualize a calm ocean shore with the waves coming in smoothly. There's warm sand under your feet, the light from the sun warming your skin, and the faint sound of seagulls. Now imagine you're carrying a small pail or bucket. You put all your worries and anxieties in that bucket, then drop it at the edge of the water and watch it float away until it's out of sight. This is called ocean dumping. 

2.  Take a short walk outside when you feel overwhelmed, and try to start exercising. Exercising and physical movement help release endorphins, which can help you stay alert and is a natural way to regulate stress.  

3. Play music while you're studying. Some people find it useful to listen to something with a regular, steady beat, like reggae or hip-hop. These types of music have a mathematical rhythm and can help your learning process. If you don't want to listen to music, try a recording of ocean sounds, rain sounds, or white noise. 

4. If you find it difficult to handle stress on your own, consider seeing a counselor. They can give you more tips on controlling your stress and studying effectively. 

Of course, as the date for the test gets closer and closer, you might be struggling with anxious thoughts. The best thing to do is to slowly decrease how often you study as the date approaches. This might seem counterproductive, but research shows that spending the last few days before the test cramming and studying can be detrimental. Instead, do something that makes you happy, like seeing a movie or hanging out with friends. Keep the test out of your mind!

5. Finally, work carefully and patiently during the test, remember to take deep, clear breaths, and use your test-taking strategies. 

Below are examples of SAT math problems that you can use to practice. Most of them are very similar to the ones that the College Board has put out for practice, along with answer explanations with a few more tips for solving. 

Example problems that you should be able to solve - No calculator section

Multiple choice questions

1) A line, r, goes through two points: (6, -9) and (5, 2). If line r is translated down four units and right seven units, what is the slope of the new line? 

A. 11

B. -11

C. -15/7

D. 15/7

How to solve: 

Use the slope formula m = (y₂ - y₁)/(x₂ - x₁) and substitute in the given points. 

m = 2 - (-9) / 5 - 6 

m = 11/-1

m = -11

Answer: 

B. -11/1 or -11

Explanation: A common strategy to solve this question is to subtract four from the y-values of the points and add seven to the x-values of the points and then try to find the slope of the new line. However, the key to solving this problem is recognizing that a line translated means the line is simply shifted to a different spot on the coordinate plane. Therefore, we can just use the points we are given, find the change in y over the change in x, and get the correct answer. Recognizing this will also help save time and minimize the margin for error. 

2) The amount of water, given in gallons, in a leaking plastic swimming pool can be estimated by the equation y = -5.8529x + 10,000, where x represents time in minutes since 2:00 pm. What is the best interpretation of the number -5.8529, when considering the context of this problem? 

A. The time in minutes since 2:00 pm

B. The amount of water in gallons in the swimming pool since 2:00 pm

C. The estimated rate of water loss per minute

D. The amount of water in gallons before the leak

Answer: 

C. The estimated rate of water loss per minute. 

Explanation: If you encounter a problem similar to this one, your biggest challenge will be the answer choices. It's important to read them carefully and determine which information given in the problem is relevant to what is being asked. A tip is to be familiar with the meaning of the components of the different formulas you can encounter on the test. For example, if you know that the m in the formula y = mx + b is always the slope and that the slope is the rate of increase or decrease, you can easily and quickly solve this type of problem. 

3) If w = 5y - 2y³ + 9 and x = 8y² - 4y + 2, what is 6x - 2w in terms of y? 

A. 4y³ + 48y² - 34y - 6 

B. 4y³ + 52y² - 34y - 6 

C. -12y³ - 16y² + 38y + 50

D. 12y³ - 16y² - 38y + 50

How to solve: 

Replace x with 8y² - 4y + 2 and w with -2y³ + 5y + 9 in 6x - 2w

6(8y² - 4y + 2) - 2(-2y³ + 5y + 9) 

Use the distributive property and combine like terms. 

48y² - 24y + 12 + 4y³ - 10y - 18

4y³ + 48y² - 34y - 6

Answer: 

A. 4y³ + 48y² - 34y - 6

Explanation: The skills tested in this question are substituting and simplifying polynomials. Studying the basics of mathematical properties, like the distributive property and combining like terms, will help solve problems of this kind. It's important to be systematic and careful when solving problems like this one. If you don't keep track of how you combine the different terms, it's very easy to start mixing them up. 

4) If a^3/2 = x, what is a in terms of x? 

A. (square root of x cubed) 

B. x² 

C. (the third root of x squared)

D. x³ 

How to solve: 

Apply exponent rules. 

a^3/2 = x

√(a³) = x

[√(a³)]² = x²

a³ = x²

a = third root of x² 

Answer:

C. (the third root of x squared)

Explanation: This question requires a good knowledge of exponent rules and how to use them. There are many ways to approach this problem, but as long as you know the basics, you should be well prepared. 

5) What is the following complex number system equal to? (Note: i² = -1) 

(12i - 4)(10 + 8i)

A. 88i - 136 

B. -42

C. 88

D. 88i - 56

How to solve: 

Use the distributive property and combine like terms. 

(12i - 4)(10 + 8i) 

120i + 96i² - 40 - 32i

96i² + 88i - 40

96(-1) + 88i - 40

88i - 136

Answer: 

A. 88i - 136

Explanation: To solve this problem, the distributive property needs to be used. You also need to be able to use i² correctly and understand what a complex number, i, represents, namely the square root of -1. 

6) Benedicte is making bracelets and earrings for her small business. Bracelets cost $1.50 to make, and a pair of earrings cost $1.25 to make. Each bracelet needs one string and each pair of earrings needs two strings. She has a maximum budget of $150.00. She has a package of jewelry strings with 600 strings. Ideally, she wants the ratio of bracelets to pairs of earrings to exceed 2 to 1. 

Write a set of inequalities to represent these conditions, if b is the number of bracelets and e is the number of pairs of earrings. 

A. 1.25b + 1.5e ≤ 150.0

1b + 2e ≤ 600

b > 2e

B. 1.5b + 1.25e ≤ 150.0

1b + 2e ≥ 600

2b > e

C. 1.5b + 1.25e ≤ 150.0

1b + 2e ≤ 600

b > 2e

D. 1.5b + 1.25e ≤ 150.0

1b + 2e ≤ 600

2b > e

Answer: 

C. 1.5b + 1.25e ≤ 150.0

1b + 2e ≤ 600

b > 2e

Explanation: The first inequality should tell us something about the maximum amount of money she's spending, so the cost of the bracelets plus the cost of the earrings has to be less than or equal to her total budget. The second inequality tells us about how much string she can use, so the amount of string she uses for the bracelets plus the amount of string she uses for each pair of earrings has to be less than or equal to 600. 

The last inequality we can solve by setting up the ratio as a fraction as shown below 

b / e > 2 / 1 

b > 2e

7) What are the solutions to 3x² - 7x + 2 = 0? 

A. x = 12 and x = 4

B. x = 1/4 and x = 2 

C. x = 1/3 and x = 4 

D. x = 1/3 and x = 2 

How to solve: 

Use the quadratic equation. 

x = [-b ± √(b² - 4ac)] / 2a 

x = [-(-7) ± √((-7)^2 - 4×3×2)] / 2(3)

x = [-(-7) ± √((-7)^2 - 24)] / 6

x = [7 ±  √(49 - 24)] / 6 

x = [7 ±  √(25)] / 6 

x = (7 ± 5) / 6

x = (7+ 5)/6 = 12/6 = 2 

or

x = (7- 5)/6 = 2/6 = 1/3 

Answer:

D.
x = 1/3 and x = 2

Explanation: Memorize the quadratic formula! It might become necessary to use it on the non-calculator section, and it's NOT going to be provided on the formula sheet. It's also important to learn how to use it. Become familiar with what the letters a, b, and c mean, and how to recognize them in a quadratic equation. 

Grid-in questions 

8) A function f(x) is defined for all real numbers by the following equation

f(x) = (3x^2 + 4) / 2. What is f(f(2))?  

How to solve: 

Find f(2). 

f(2) = (3(2)² + 4) / 2 

f(2) = (3(4) + 4) / 2 

f(2) = 16 / 2

f(2) = 8

Find f(f(2)), or f(8). 

f(8) = (3(8)^2 + 4) / 2 

f(8) = (3(64) + 4) / 2

f(8) = 196 / 2 

f(8) = 98

Answer: 98

Explanation: Some questions with functions require only a knowledge of how to substitute a value into an equation. The only catch with this question is that you have to use the value you got from the first step in the second step to answer what the problem is asking. 

9) Nate is baking a giant souffle for a contest. The souffle has risen to 1 1/2 inches over the brim of the dish after 18 minutes in the oven. Assuming that the souffle is rising at a constant rate, after how many minutes will the souffle rise to 4 1/2 inches over the brim of the dish? 

How to solve: 

The non-calculator section may require a certain level of reasoning skills. 

1 1/2 inches = 18 minutes 

Therefore...

3 inches = 36 minutes 

Therefore...

1 1/2 inches + 3 inches = 18 minutes + 36 minutes

4 inches = 54 minutes

You could also set up a proportion to solve the problem. 

1 / 12 = 4.5 / x 

x = 54 

Answer: 54 minutes

Explanation: As shown above, this question mostly just requires good reasoning skills. It is possible to set up a proportion to solve it right in the beginning, but dealing with fractions and decimals in a proportion without a calculator might lead to issues if you aren't careful. 

10) If (x)^-1 = 4, what is (x)^-2? 

How to solve: 

Rule: (x)^-1 = 1/x

(x)^-1 = 4

x = 1/4 

(x)^-2

1/x² 

1/(1/4)² 

1/(1/16)

16

Answer: 16 

Explanation: Using the exponent rule, this question is quite simple to solve. While it may seem difficult to follow, the steps are really a formality. A good knowledge of the exponent rule makes this one of the easier questions here. 

Example problems that you should be able to solve - Calculator section 

Multiple choice questions

1) At the local aquarium, the mean age of the male penguins is 8 years old, and the mean age of the female penguins is 5 years old. What is true about the mean age m of the combined group of penguins at the aquarium? 

A. m = 13

B. m <  6.3

C. 5 < m < 8

D. m < 5 

Answer: 

C. 5 < m < 8

Explanation: This question is interesting because it doesn't require any calculations to get the correct answer, only the ability to reason using the concept of mean. The biggest mistake you can make on this question is finding the mean of the two means.

Mean age of the male penguins is 8

Mean age of the female penguins is 5

For the sake of argument, suppose the mean age of female penguins is also 8. Then the combined mean is also 8. However, in reality the mean age of the female penguins is smaller than 8. Therefore, the combined mean cannot be bigger than 8. It has to be smaller than 8 

By the same token, suppose the mean age of male penguins is also 5. Then the combined mean is also 5. However, in reality the mean age of the male penguins is bigger than 5. Therefore, the combined mean cannot be smaller than 5. It has to be bigger than 5. 

2) A function f is defined by f(x) = 4x³ - 2x² + cx - 5. The function goes through the points (0,-5), (p, 0), and (2,25). What is the value of c? 

A. 3

B. -5 

C. 1

D. 2

How to solve: 

Set one of the given points in and solve for c. Use (2, 25)

f(x) = 4x³ - 2x² + cx - 5 

25 = 4(2)³ - 2(2)² + c(2) - 5 

25 = 32 - 8 + 2c - 5 

25 = 19 + 2c 

6 = 2c 

3 = c 

Answer: 

A. 3

Explanation: A good understanding of how to evaluate polynomial functions is important to solve this problem. The best way to solve this problem is to use the points given. However, some of the points are there to trick you. If you use the point (0,-5), you'll actually cancel out c, the value you are trying to find. Notice also that if you use p, you will get c in terms of p. However, your answer must be a number, not a variable. 

3) Jamie is visiting Norway and buys a souvenir cup for his mom. He gets a 15% discount and pays k kroner, including a 25% sales tax on the discounted sales price. Write an expression that expresses the original price, p, of the cup in terms of k. 

A. p = k * 0.85 * 1.25

B. p = k / (0.85 * 1.25) 

C. p = k / (0.85 * 0.25) 

D. p = k * 0.85 * 0.25

Answer: 

B. p = k / (0.85 * 1.25) 

Explanation: The biggest mistake you can make on this problem is misunderstanding what the question is asking for. It might be easy to think that you have to look for how much Jamie paid for the cup, but the question is looking for the original price, meaning you have to set your solution up differently. 

Always reread and make sure you truly understand what you are looking for. 

4) In a fictional town in Norway, approximately 2 in 7 people have green eyes. If the population of the town is about 856,000, approximately how many people have green eyes?  

A. 428,000

B. 214,000

C. 122,000

D. 245,000

How to solve: 

Set up a proportion and solve. 

2 / 7 = x / 856,000

7x = 1,712,000

x ≈ 245,000

Answer: 

D. About 245,000 people

Explanation: There are several ways to solve this problem, but knowing how to set up a proportion can help you to solve it faster. A proportion allows you to write a comparison between a part and a whole. In this example, we have 2 as the part. So for every 7 people, 2 people have green eyes. We write a proportion to apply this value to a larger population. x people have green eyes in a whole population of 856,000 people. 

Once we set it up, we cross multiply and solve for x, which gives us a value of about 245,000 people in the town who have green eyes. 

5) A school canteen sells club sandwiches for $5.99 and iced teas for $2.99. At the end of the day, the canteen has made $487.85 from selling a total of 115 items. How many sandwiches did they sell? 

A. 48

B. 56

C. 67

D. 88

How to solve: 

1. Set up your system of equations and solve it. 

x = sandwiches 

y = iced teas

5.99x + 2.99y = 487.85

x + y = 115

y = 115 - x

5.99x + 2.99(115 - x) = 487.85 

5.99x + 343.85 - 2.99x = 487.85

3x = 144

x = 48 

Answer: 

A. 48 sandwiches

Explanation: Knowing how to solve systems of equations is an essential skill. If you can set one up correctly, using variables to represent the unknown values, you're well-equipped to solve a problem like this easily and quickly. 

When easy problems like this one come up, solve them first. This will give you a little boost of confidence to handle the ones that aren't so easy. 

6) Rebecca's car gets 29 miles per gallon. If gas costs $3.56 per gallon, how much would it cost for her to drive from Tallahassee, Florida, to Key West, Florida, if the distance between the two cities is about 641 miles?  

A. $81.50

B. $77.35

C. $67.52 

D. $78.68 

How to solve: 

641 miles / 29 miles per gallon = 22.1 gallons of gas 

22.1 gallons * $ 3.56 per gallon = $ 78.68 for gas

Answer: 

D. $78.68

Explanation: This problem requires no other skills than simple multiplication, division, and application of mathematical concepts to everyday life. Again, try to get these simpler questions correct quickly, because it will give you a boost of confidence to solve the ones that are a bit harder. 

7) The sum of two positive integers is 20, and the difference between these numbers multiplied by 2 is 12. What is the product of these two numbers? 

A. 7

B. 13

C. 91

D. 20

How to solve: 

Set up and solve a system of equations with two unknowns. 

x + y = 20 

2(x - y) = 12 

x = 20 - y 

2[(20 - y) - y] = 12 

2(20 - 2y) = 12 

40 - 4y = 12 

-4y = -28 

y = 7 

x + y = 20 

x + 7 = 20 

x = 13 

13 * 7 = 91 

Answer: 

C. 91 

Explanation: Again, it's important to make sure you find exactly what the question is asking for. You have to be sure to find the product of the two numbers at the end. It's also important to set up the problem correctly, exactly the way it's stated in the word problem. 

Grid-in questions

8) If 12 - 7x is 9 more than 4, find the value of 6x. 

How to solve: 

12 - 7x = 4 + 9 

12 - 7x = 13 

-7x = 1 

x = -1/7

6x = 6(-1/7) = -6/7

Answer: -6/7

Explanation: The terms used in this problem can easily be intimidating at first glance. You might be confused by the use of "is" and "more than," because they aren't typically used to say "equal to" and "add." 

You also have to remember that the problem is asking you to find 6x, not just x.

9) Roy, Colin, and Sam were shooting penalty kicks at soccer practice today. Colin scored two-thirds as many times as Sam, and Roy scored half as many times as Colin. They scored a total of 96 goals. How many goals did Sam score? 

How to solve: 

Use one letter to represent the goals Sam scored, for example, g. 

*2/3g represents the number of goals Colin scored. We then put Roy's goals in terms of Sam's goals so we can combine like terms: 1/2(2/3g) = 2/6g = 1/3g.*

g + 2/3g + 1/3g = 96 

3/3g + 2/3g + 1/3g = 96

6/3g = 96

2g = 96 

g = 48

Plug g back into your original equation to double-check. 

g + 2/3g + 1/3g = 96 

(48) + 2/3(48) + 1/3(48) = 96

48 + 32 + 16 = 96 

96 = 96 

Answer: 48 goals

Explanation: It's easy to get confused by the fractional terms in this problem. Using only one unknown will greatly simplify your work and help you go through the test more efficiently. In reality, the math in this problem isn't difficult at all. As long as you set up your equation correctly, you can succeed at this type of problem. 

10) When a = 12 and b = 9, by much does the value of 3a² + 2b exceed the value of 2b² + 3a ?

How to solve: 

Solve each expression separately. 

2b² + 3a

2(9)² + 3(12)

2(81) + 36

162 + 36

198 

3a² + 2b

3(12)² + 2(9)

3(144) + 2(9)

432 + 18

450

450 - 198 = 252

Answer: 252

Explanation: This question requires a knowledge of algebra and evaluating an expression with two unknowns. The biggest mistake you can make on this problem is a calculating error with the various values you have to keep track of.