Absolute Value of a Complex Number
The absolute value of a complex number a + bi, also called the modulus of a complex number a + bi, is its distance from the origin on the complex number plane.
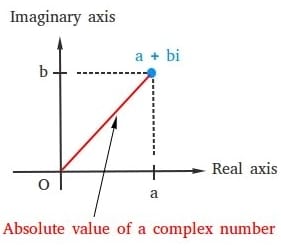
On the complex plane, the complex number a + bi is represented as a point (a, b) and the coordinate of the origin is (0, 0).
Just find the distance between (0,0) and (a,b)
We can use the distance formula to find the absolute value of a complex number.
$$ Distance =
\sqrt{(a-0)^{2}+(b-0)^{2}}$$
$$ Distance =
\sqrt{(a)^{2}+(b)^{2}}$$
$$ |a + bi| =
\sqrt{(a)^{2}+(b)^{2}}$$

Two examples showing how to find the absolute value of a complex number.
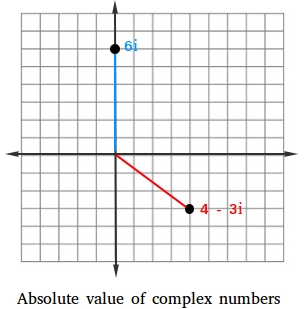
Find the absolute value of the complex numbers 4 - 3i and 6i.
Notice that 6i = 0 + 6i.
$$ |4 - 3i| =
\sqrt{(4)^{2}+(-3)^{2}}$$
$$ |4 - 3i| =
\sqrt{16 + 9} = 5 $$
$$ |6i| =
\sqrt{(0)^{2}+(6)^{2}}$$
$$ |6i| =
\sqrt{0 + 36} = 6 $$
The figure below shows the distance for the complex number 4 - 3i in red and the distance for the complex number 6i in blue.