Angle Bisector
Angle Bisector Visualization
Instructions
Drag the blue control points on the rays to adjust the angle
Use the slider or input field to set a specific angle
The red ray shows the angle bisector, which divides the angle into two equal parts
For angles greater than 180°, the bisector divides the reflex angle
What is an Angle Bisector?
An angle bisector is a ray that divides an angle into two congruent angles or two angles that have the same measure.
For example, in the figure below, ray OB shown in red is an angle bisector and it divides angle AOC into two congruent angles.
These two congruent angles are angle AOB and angle COB.
Notice that within the ray, segment OB has the same endpoint as ray OB. Therefore,
It is perfectly ok to say that the ray or the segment bisects angle AOC.
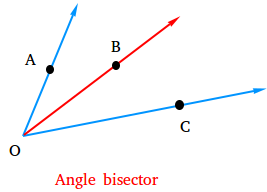
Learn how to find an angle bisector by reading this lesson.
Angle bisector of a triangle
An angle bisector of a triangle is a segment that bisects an angle of that triangle and extends to the opposite side.
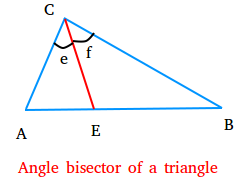
In triangle ABC shown above, segment CE is an angle bisector for that triangle.
Segment CE bisects angle ACB and creates angle ACE and angle BCE that are congruent.
You could also say that m∠e = m∠f