Area of a Rhombus

You will learn here to find the area of a rhombus when the lengths of the diagonals are not given explicitly. You will need to use a property of the rhombus and knowledge that you have about Pythagorean triples.

Example

Use the rhombus ABCD below in order to find the area of the rhombus.

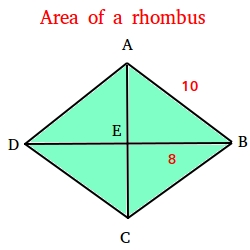
The formula to use to find the area of a rhombus is area = 0.5(d₁× d₂), where d₁ and d₂ are the lengths of the diagonals.

Notice that d₁ could be, for example, the length of AC and d₂ could be the length of DB.

Notice also that EB is equal to 8. Furthermore, we know that the diagonals of a rhombus bisect each other. This means that segment AC bisects DB. We can then conclude that DE is also equal to 8. Therefore, DB = DE + EB = 8 + 8 = 16.

Now we need to find the length of AC.

Since AC is a perpendicular bisector, triangle ABE is a right triangle with AB = 10 and EB = 8.

(3, 4, 5) is a Pythagorean triple. If we multiply each number by 2, we get another Pythagorean triple or (6, 8, 10).

8 and 10 are parts of a Pythagorean triple whose missing third number is 6.

Therefore, using a Pythagorean triple, AE is equal to 6.

Lastly, BD bisects AC. We can then conclude that EC is also equal to 6.

Therefore, AC = AE + EC = 6 + 6 = 12.

d₁ = AC = 12 and d₂ = DB = 16

Area = 0.5(d₁× d₂)

Area = 0.5(12 × 16)

Area = 0.5(192)

Area = 96