Checkerboard puzzle
Take a look at the checkerboard below. A typical checkerboard puzzle could ask you the following question:How many squares, of all sizes, are there on this 8 × 8 checkerboard? However, isn't it important to know how many different sizes are there?
The different sizes are 1 × 1, 2 × 2, 3 × 3, 4 × 4, 5 × 5, 6 × 6, 7 × 7, and 8 × 8

In this checkerboard puzzle, it is easy to know how many 1 × 1 there are. Since there are 8 such square on each size, there are a total of 8 × 8 = 64
It is also easy to see that there is only 1 square that has a size of 8 × 8
To find out how many there are for any other size is a big headache. However, I will illustrate the technique or trick for 2 sizes, the 2 × 2 and the 6 × 6.
I leave it up to you to find it for the remaining sides! And if you do find it, I am happy.
First, let us find out how many 2 × 2 there are. You will need to carefully examine the following illustration:
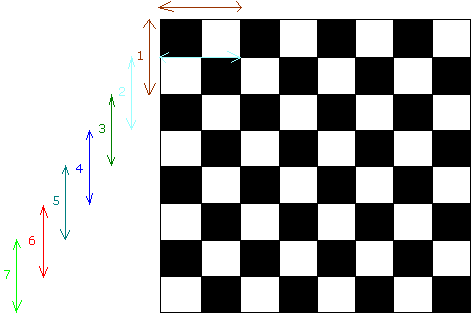
I carefully numbered all the 2 × 2 squares we can get on one side starting from the very top and going down 1 unit each time
Since there are 7 such square on one side, we know there will be 7 such square on any other side.
since 7 × 7 = 49, 49 squares have a size of 2 × 2
Next, let us find out how many 6 × 6 there are. Again, you will need to carefully examine the following illustration:
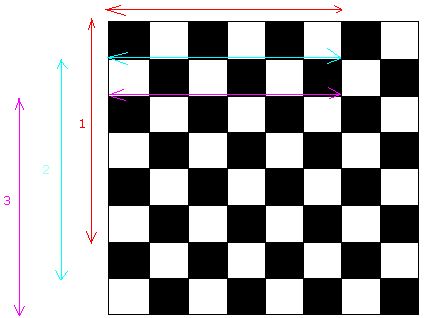
I carefully numbered all the 6 × 6 squares we can get starting from the very top and going down 1 unit each time
Since there are 3 such square on one side, we know there will be 3 such square on any other side.
since 3 × 3 = 9, 9 squares have a size of 6 × 6
Following a similar course, there are
36 squares with a size of 3 × 3
25 squares with a size of 4 × 4
16 squares with a size of 5 × 5
4 squares with a size of 7 × 7
Adding the values of all sizes, we get 64 + 1 + 49 + 9 + 36 + 25 + 16 + 4 = 204
Therefore, there are 204 squares of sizes 1 × 1, 2 × 2, 3 × 3, 4 × 4, 5 × 5, 6 × 6, 7 × 7, and 8 × 8
Have fun with this checkerboard puzzle! Any questions? contact me using the form in about me