What is a complex number ? Definition and examples
A complex number is any number that can be written in the form a + bi where a and b are real numbers. a is called the real part, b is called the imaginary part, and i is called the imaginary unit.
Where did the i come from in a complex number ? A little bit of history!
Because the square of a real number is never negative, there is no real number x such that x2 = -1. Mathematicians wanted this equation to have a solution.
Therefore, they defined i to be the solution of the equation x2 = -1 and called i imaginary number or imaginary unit. By doing this, they invented a new system of numbers called complex numbers.
What they basically did is this.
Let √-1 = imaginary number = i since such number does not exist with real numbers, but exist only in our imagination. Then, we can just call it complex number.
Now we use complex numbers in electromagnetism, signal processing, and many others!
A new system of numbers entirely based on the the imaginary unit i
Since i = √-1, we can then express the square root of any negative number as a real multiple of i.For example, √-36 = √(36 × -1) = √36 × √-1 = 6i
In general, for any positive real number a, √(-a) = (√a) i
What is the difference between a complex number and an imaginary number?
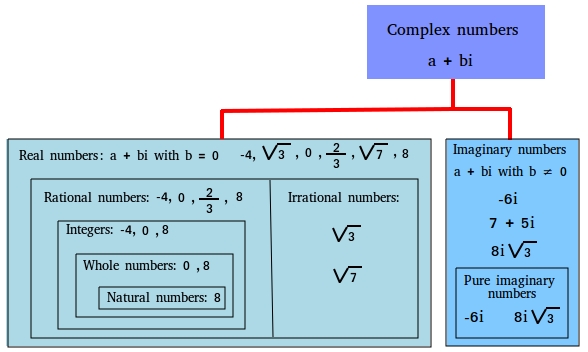
Consider again the complex number a + bi. If a is not equal to 0 and b = 0, the complex number a + 0i = a and a is a real number. Therefore, all real numbers are also complex numbers.
If b is not equal to zero and a is any real number, the complex number a + bi is called imaginary number.
In other words, if the imaginary unit i is in it, we can just call it imaginary number.
If the imaginary unit i is in t, but the real real part is not in it such as 9i and -12i, we call the complex number pure imaginary number.
What is a complex number? Still confused?
Here is a diagram that shows the difference between a complex number, a real number, an imaginary number, and a pure imaginary number.