Components of a vector
The components of a vector are the resulting vectors after the projection of the vector on the x, y, and z axes. For example, if you project the vector shown in blue below on the x-axis, the component will lie on the x-axis.
One way we can easily find the components of a vector is by putting the tail or
initial point of a vector at the origin of a coordinate system. Let us project vector A shown below in blue on the x-axis and y-axis.
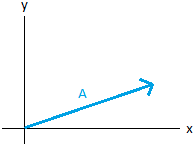
We find the components by drawing perpendicular lines from the head or terminal point to the axis. The vectors shown in red are the components of vector A.
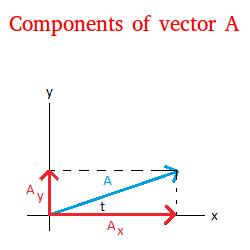
The process of finding the components of a vector is called resolving the vector
Equations for the components of a vector
Some simple trigonometry can help us find some equations for the components and the angle t.
Ax = A cos(t)
Ay = A sin(t)
The components of a vector are given by
Ax = A cos(t)
Ay = A sin(t)
To find the magnitude of A, we can use the pythagorean theorem.
A = √((Ax)2 + (Ay)2)
A real life example showing how to find the components of a vector
A drone leaves a house and is later sighted 8 kilometers away in a direction making an angle of 60 degrees north of east. How far east and north is the drone from the house when sighted?
Solution:
The key idea here is that we are given the magnitude (8 km) and the angle or direction (60 degrees north of east) of the vector.
Now we need to resolve the vector or find its components.
Put the vector in an xy coordinate system and for convenience, the origin is placed at the house.
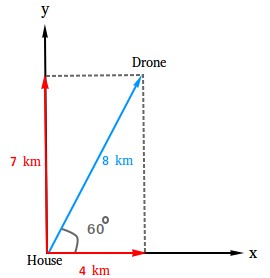
Ax = A cos(t)
Ax = 8 × cos(60)
Ax = 8 × 0.5
Ax = 4 km
Ay = A sin(t)
Ay = 8 × sin(60)
Ay = 8 × 0.866
Ay = 6.928 km
Ay is closely equal to 7
The drone is 4 kilometers east and 7 kilometers north of the house.