Compound inequality

A compound inequality is a statement in which two inequalities are connected by the word "and" or the word "or".

For example, x > 5 and x ≤ 7         and        x ≤ -1 or x > 7 are examples of compound inequalities

When the word that connects both inequalities is "and", the solution is any number that makes both inequalities true.

When the word that connects both inequalities is "or", the solution is any number that makes either inequalities true.

For example, graph the following compound inequality: x ≥ 2 and x < 4

The graphs for x ≥ 2 and x < 4 should look like this:




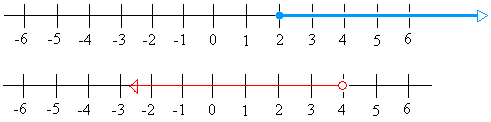
Putting the two graphs together gives the following:




The solution is that portion of the graph where you see red and blue at the same time( Or the portion shaded twice)

If you pull this out from the graph above, we get:




This means that the solution is any number between 2 and 4, to include 2, but not 4.

Notice that the open circle (in red) means that 4 is not included

Graph x ≥ - 2 and x > 1

The graphs for x ≥ - 2 and x > 1 should look like this:




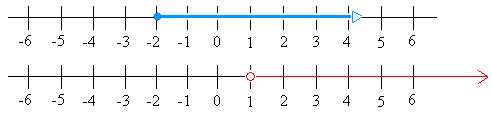
Putting the two graphs together gives the following:




The solution is that portion of the graph where you see red and blue at the same time( Or the portion shaded twice)

If you pull this out from the graph above, we get:




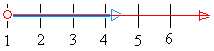
The solution is any number after 1

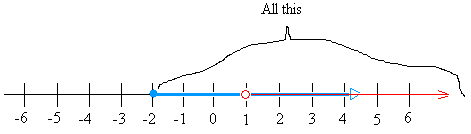
However, if we twist the same problem above and graph x ≥ - 2 or x > 1, it is a different story.

Since the "or" means either, the solution will be the shaded area that include both inequalities.

The solution is thus any number after -2



Graph x > 2 or x < -3


Here it is!



However, if for the same problem right above, I replace "or" by "and", there will be no solutions for this compound

Look carefully again at the graph right above and you will see that blue and red don't meet. That is why they have nothing in common and thus no solutions.