Constructing  perpendiculars

Constructing perpendiculars to a line through a specific given point using only a straightedge and a compass is what I will show you here. There are two cases that you may encounter.

Case #1: You are given a line and a point on the line.



Case #2: You are given a line and a point not on the line.


We will demonstrate both cases.

Constructing perpendiculars: Let us start with case #1.

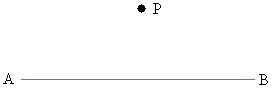
Step #1

Start with the following line and point P



Open your compass to any radius or distance. Put the needle of the compass at point P and draw arcs on both sides of point P. Label the points where the arcs intersect the line C and D.


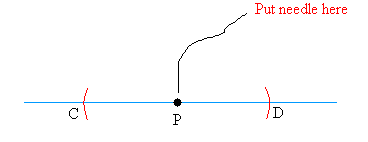
Step #2

Open your compass to a radius or distance greater than the distance you chose to draw the arcs.

After you have increased your compass opening, place the needle at C and draw and arc.

Then, still using the same compass opening place the needle at D and draw another arc.

The two arcs should intersect as shown below. Call the point the two arcs intersect E.



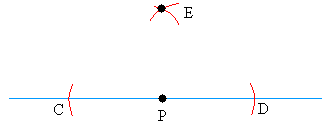
Step #3

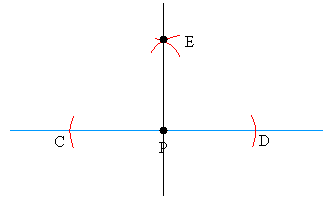
Draw a line between P and E and you are done!

Constructing perpendiculars: case #2.

Case #2: You are given a line and a point not on the line.

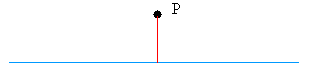
Start with the following line and point P not on the line.


Step #1

Open your compass to a radius or distance greater than the distance from P to the line.

The distance you see below in red is the shortest distance from P to the line. That is what I mean by distance from P to the line; It is the shortest distance from P to the line which is usually done by drawing a straight line down.


Open you compass to a distance greater than that.

Step #2

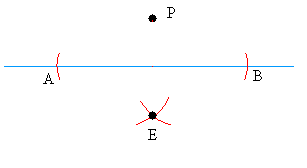
After opening your compass to a distance greater than the shortest distance from P to the line, place the needle of the compass at P and draw arcs that intersect the line in two places.


Call the points the arc intersect the line A and B

Step #3

Keeping the opening of the compass the same, place the needle at A and draw and arc.

Then, place the needle at B and draw an arc. Call the point the two arc intersect E.


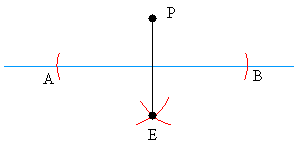
Step #4

Draw a line between point P and point E and you are done!


Here we go! Make sure you understand each step outlined above and follow them carefully. If you do this, you will have no problems whatsoever constructing perpendiculars.