What is a deficient number?
In number theory, a deficient number is a number in which the sum of its proper factors is less than the number.
Examples explaining what a deficient number is.
For example, the number 4 is deficient. The proper factors of 4 are 1 and 2. Since 1 + 2 = 3 and 3 is smaller than 4, 4 is deficient.
Notice that 4 is not included among the proper factors of 4.
15 is also deficient.
The proper factors of 15 are 1, 3, and 5. Since 1 + 3 + 5 = 9 and 9 is smaller than 15, 15 is deficient.
42 is not a deficient number.
The proper factors of 42 are 1, 2, 3, 6, 7, 14, 21.
Notice that 1 + 2 + 3 + 6 + 7 + 14 + 21 = 54. Since 54 is bigger than 42, 42 is not a deficient number.
In order for a number to be a deficient number, the sum of the proper factors of the number must be smaller than the number, not greater, or equal to the number.
The first 20 deficient numbers are 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 21, 22, 23, and 25.
From the list above, you can clearly see that all the prime numbers from 1 to 25 are included in the list. Having said that we can say with confidence that all prime numbers are also deficient numbers.
Did you not quite understand the examples above? Do you need more explanations? Take a look at the figure below that summarizes everything.
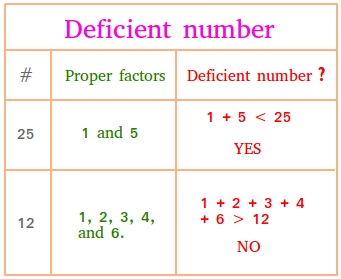
Why all prime numbers are also deficient numbers?
The reason that all prime numbers are deficient numbers as well is because the sum of all proper factors of a prime number is always going to be 1.
For example, 401 is a prime number since 401 can only be divided by 1 and 401.
The only proper factor for this prime number is 1 since 401 cannot be included when we perform the test of adding the proper factors.
By the same token, 73 is a prime number since 73 can only be divided by 1 and 73.
The only proper factor for this prime number is 1 since 73 cannot be included when we perform the test of adding the proper factors.