Definition of Absolute Value

Definition of absolute value: The absolute value of a number is the distance the number is from zero. Take a look at the following two graphs: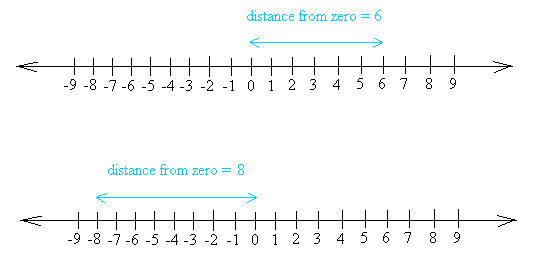

The first graph shows 6 located at a distance of 6 units from zero.
Then, the absolute value of 6 is 6 and we write |6| = 6

The second graph shows -8 located at a distance of 8 units from zero.
Then, the absolute value of -8 is 8 and we write |-8| = 8.

Therefore, do not write |5| = -5 or |4| = -4 please!

|6| means distance from 0 to 6.

|-8| means distance from 0 to -8.

For |-8| = 8, you could also argue that to get 8, you have to take the negative of -8 since - - 8 = 8

So, | - 8| = - - 8 = 8.

This observation helps us to come up with a formal definition of absolute value.

| x | = x if x is positive or zero, but -x if x is negative.

This definition is important to understand before solving absolute value equations or absolute value inequalities.

Other examples helping us to apply the definition of absolute value

Calculate the absolute value of the following numerical expressions.

1) -8 + 2 × 5

2) 4² − 4 × 2

3) -5 + 5 × 2 − 15

1)

| -8 + 2 × 5 | = | -8 + 10 |

| -8 + 2 × 5 | = | 2 |

| -8 + 2 × 5 | = 2

2)

| 4² − 4 × 2| = | 16 − 4 × 2|

| 4² − 4 × 2| = | 16 − 8|

| 4² − 4 × 2| = | 8 |

| 4² − 4 × 2| = 8

3)

|-5 + 5 × 2 − 15| = | -5 + 10 − 15 |

|(-5 + 5 × 2 − 15)| = | 5 − 15 |

|(-5 + 5 × 2 − 15)| = | -10 |

|(-5 + 5 × 2 − 15)| = 10