Difference between a Ratio and a Fraction

There is a difference between a ratio and a fraction even though students usually think there is none. 

It is true that we can simplify a ratio the same way we simplify a fraction. For example, the ratio 6 to 9 or 6 / 9 is equivalent to the ratio 2 to 3 or 2 / 3.

However, ratios do not always follow the same rules as fractions.

Do you understand the figure below? Is it still confusing? Keep reading so the difference between a ratio and a fraction becomes very clear 

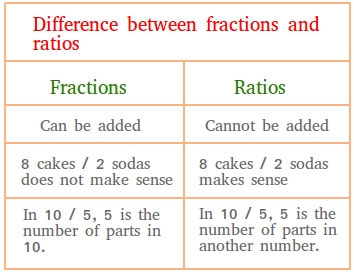
1. We do not add or subtract ratios although we can add or subtract fractions.

• For instance, trying to add the following two ratios is just plain nonsense. 
  3 books / 8 pens and 6 books / 5 pens

2. A ratio does not always compare things that have the same units although a fraction compare things with the same units. With ratios, the units may or may not be the same.

• For example, the fraction 8 cakes / 2 sodas does not make sense. Why not? It is because this will mean that we are trying to find out how many sodas can go into 8 cakes. Nonsense!
  
  
• However, the ratio 8 cakes / 2 sodas make perfect sense even though the units are not the same. The ratio 8 cakes / 2 sodas just tells us that for every single soda, there are 4 cakes since 8 cakes / 2 sodas is also equal to 4 cakes / 1 soda.  

• Similarly, the ratio 40 miles to 2 gallons or 20 miles to 1 gallon makes perfect sense if you are trying to see how far you can go with 1 gallon of gas.

• The ratio 20 cakes / 15 cakes also makes perfect sense if you are comparing the number of cakes you made to the number of cakes your neighbor made in a given year.

3. The denominator in a fraction usually represents the number of parts in the same whole.

• For example, in the fraction 8 biscuits / 4, 4 represents the number parts in the same whole or 8 biscuits.
  
  
• However, suppose a bag has 80 red balls and 50 blue balls. The ratio 80 / 50 can be simplified to 8 / 5. In the ratio 8 / 5, the denominator 5 represents the number of parts in another whole and that whole is the number of blue balls, not the number of red balls.