Distance and displacement

There is a difference between distance and displacement. Take a close look at the following illustration that will clearly show the difference between the two.

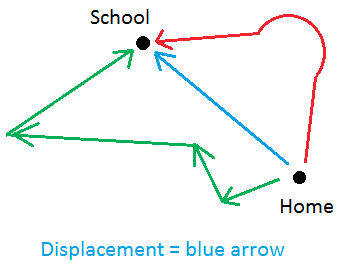
As you can see in the illustration above, the displacement is the straight-line path between home and school.

The green path or the red path on the other hand is the distance or distance traveled.

Did you notice that the magnitude of the displacement is not always the same as the distance traveled?

In fact, the displacement is the shortest path from one location to another with no left turn, right turn, or going around a curve.

Notice that when something is being displaced, it will have a direction associated with it. Therefore, displacement is a vector. 

Mathematical representation of displacement and formula

To represent displacement, the letter s is used with an arrow of top of the s as shown below.

s→

Displacement = final position - initial position

Let X_f = final position and X_i = initial position

Displacement = X_f - X_i