Divisibility rules

This lesson presents divisibility rules, also called divisibility tests, for the numbers 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, and 13. Divisibility rules of whole numbers are very useful because they help us to quickly determine if a given number can be divided by 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, and 13 without doing long division. Read the lesson or just take the quiz to see how much you know.

This is especially useful when dealing with large numbers and/or when you are trying to find the prime factorization of a number.

Divisibility means that you are able to divide a number evenly. When a number can be divided evenly, the remainder is zero. For instance, 8 can be divided evenly by 4 because 8/4 = 2. However, 8 cannot be divided evenly by 3 because there will be a remainder(2).

8 = 3 + 3 + 2 = 2(3) + 2

To illustrate the concept, let's say you have a cake and your cake has 8 slices, you can share that cake between you and 3 more people evenly. Each person will get 2 slices.

However, if you are trying to share those 8 slices between you and 2 more people, there is no way you can do this evenly. Two people will get 3 slices of cake and one person will end up with the remainder or the leftover (2).

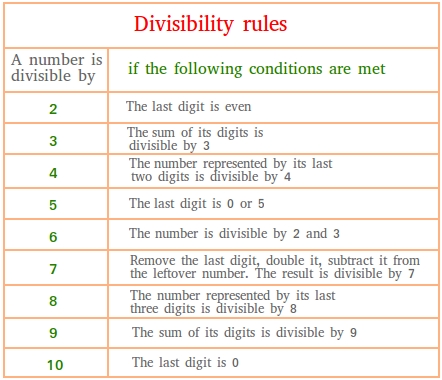
Divisibility rules and examples showing how to use the rules

Rule #1: divisibility by 2

A number is divisible by 2 if its last digit is an even number or the last digit is 0,2,4,6,or 8.

For instance, 8596742 is divisible by 2 because the last digit is 2.

Rule #2: divisibility by 3

A number is divisible by 3 if the sum of its digits is divisible by 3.

For instance, 3141 is divisible by 3 because the sum of the digits is divisible by 3.

3+1+4+1 = 9 and 9 is divisible by 3.

Rule # 3: divisibility by 4

A number is divisible by 4 if the number represented by its last two digits is divisible by 4.

For instance, 8920 is divisible by 4 because 20 is divisible by 4.

Rule #4: divisibility by 5

A number is divisible by 5 if its last digit is 0 or 5.

For instance, 9564655 is divisible by 5 because the last digit is 5.

Rule # 5: divisibility by 6

A number is divisible by 6 if it is divisible by 2 and 3. Be careful! it is not one or the other. The number must be divisible by both 2 and 3 before you can conclude that it is divisible by 6.

Rule # 6: divisibility by 7

To check divisibility by 7, subtract the double of the last digit from the remaining digits. If the difference is divisible by 7, then the original number is also divisible by 7. Repeat if necessary if the number is too big.

Is 348 divisible by 7?

Remove the last digit, which is 8. The remaining digits are 34. Double 8 to get 16 and subtract 16 from 34.

34 − 16 = 18 and 18 is not divisible by 7. Therefore, 348 is not divisible by 7.

Is 37961 divisible by 7?

Remove the last digit, which is 1. The remaining digits are 3796. Double 1 to get 2 and subtract 2 from 3796.

3796 − 2 = 3794 and 3794 is still too big. Thus repeat the process.

Remove the last digit, which is 4. The remaining digits are 379. Double 4 to get 8 and subtract 8 from 379.

379 − 8 = 371 and 371 is still too big. Thus repeat the process.

Remove the last digit, which is 1. The remaining digits are 37. Double 1 to get 2 and subtract 2 from 37.

37 − 2 = 35 and 35 is divisible by 7. Therefore, 37961 is divisible by 7.

Rule #7: divisibility by 8

A number is divisible by 8 if the number represented by its last three digits is divisible by 8.

For instance, 587320 is divisible by 8 because 320 is divisible by 8.

Rule #8: divisibility by 9

A number is divisible by 9 if the sum of its digits is divisible by 9.

For instance, 3141 is divisible by 9 because 3+1+4+1 = 9 and 9 is divisible by 9.

Rule # 9: divisibility by 10

A number is divisible by 10 if its last digit or the digit in the ones place is 0.

For instance, 522480 is divisible by 10 because the last digit is 0.

Other important divisibility tests

Rule # 10: divisibility by 11

There are a couple of ways to determine divisibility by 11.

Method #1

Subtract the last digit of the number from the rest of the number. If the difference is divisible by 11, then the entire number is also divisible by 11. Repeat if necessary until you get a two-digit number or a number that you can easily divide by 11.

For example, is 121 divisible by 11?

Subtract 1 from 12

Since 12 - 1 = 11 and 11 is divisible by 11, 121 is also divisible by 11. 

Is 1364 divisible by 11?

Subtract 4 from 136

136 - 4 = 132 

Since 13 - 2 = 11  and 11 is divisible by 11, 1364 is also divisible by 11.

Method #2

If the difference of the sum of alternative digits of a number is divisible by 11, then the entire number is divisible by 11.

Is 8195 divisible by 11?

Alternative digits are (8 and 9) and (1 and 5)

Just add them and then subtract

8 + 9 = 17

1 + 5 = 6

17 - 6 = 11

Since 11 is divisible by 11, 8195 is also divisible by 11.

Is 81972 divisible by 11?

Alternative digits are (8, 9, and 2) and (1 and 7)

Just add them and then subtract

8 + 9 + 2 = 19

1 + 7 = 8

19 - 8 = 11

Since 11 is divisible by 11, 81972 is also divisible by 11.

Rule # 11: divisibility by 12

A number is divisible by 12 if the number is divisible by both 3 and 4.

Is 180 is divisible 12?

180 is divisible by 3 since 1 + 8 + 0 = 9 and 9 is divisible 3.

180 is divisible by 4 since 80 is divisible by 4.

Therefore, 180 is divisible by 12.

Rule # 12: divisibility by 13

Add four times of the last digit of the number to the remaining number. Repeat the process if necessary until you get a number with two digits. If the number you end up with is divisible by 13, then the original number is also divisible by 13.

Is 156 divisible by 13?

4(6) = 24

24 + 15 = 39

Since 39 is divisible by 13, 156 is also divisible by 13.