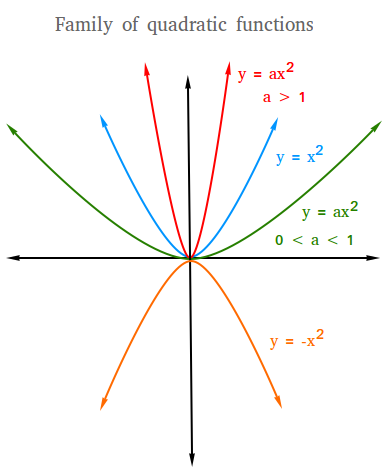
The family of quadratic functions

This lesson will summarize the family of quadratic functions using the parent function y = x²

Vertical stretch or shrink, and/or reflection in x-axis

Parent function: y = x²

Reflection in x-axis: y = -x²

Stretch by a factor of a: y = ax²

If a > 1, then the graph will stretch or become more narrow than the graph of y = x²

Shrink by a factor of a: y = ax²

If 0 < a < 1, then the graph will shrink or become more wide than the graph of y = x²

(Stretch or Shrink) and reflection in x-axis: y = -ax²

The figure below shows what the graph will look like for a stretch, shrink, or a reflection using y = x² as the parent function. Notice that the blue graph is the parent function or y = x².

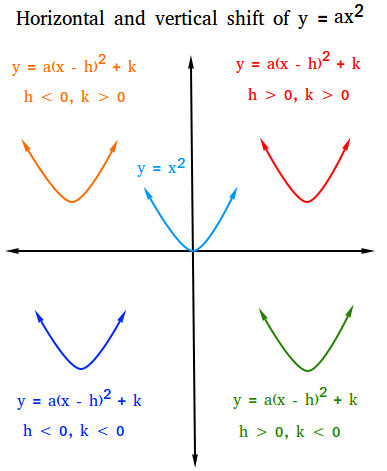
Vertex form

Parent function: y = x²

Vertex form: y = a(x - h)² + k

The vertex is (h, k) and the line x = h is the axis of symmetry.

The graph and vertex of y = ax² shifts h units horizontally and k units vertically.

For k > 0, the graph shifts up

For k < 0, the graph shifts down

For h > 0, the graph shifts to the right

For h < 0, the graph shifts to the left

The figure below shows what the graph will look like for horizontal and vertical shifts using y = x² as the parent function. Notice that the blue graph is the parent function or y = x².