Find geometric probability

Recommended for You

Not sure where to start? These are the lessons and games we recommend most to students, parents and teachers on Basic-mathematics.com. Each lesson explains the topic in plain language, walks you through worked examples step by step, and ends with practice so you can check your understanding. Pick one below, or use the menu to find lessons on fractions, algebra, geometry, statistics and more.

 In order to find geometric probability, we will use the circular dartboard shown below. 

Geometric probability using a dartboard

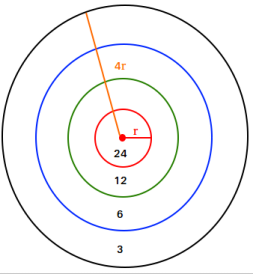
Suppose that all the points shown on the dartboard above are equally likely to be hit by a dart that you throw.

Notice the followings:

  • If your dart hit the dartboard outside the blue circle, but inside the black circle, your score is 3 points.
  • If your dart hit the dartboard outside the green circle, but inside the blue circle, your score is 6 points.
  • If your dart hit the dartboard outside the red circle, but inside the green circle, your score is 12 points.
  • If your dart hit the dartboard inside the red circle, your score is 24 points.

Find the following geometric probabilities

1. You score at least 6 points 

2. You score exactly 3 points

3. You score at the most 6 points

4. The dart lands inside the red circle

Solution

1. P(You score at least 6 points)

When you score at least 6 points, your score is 6 points, 12 points, or 24 points. The radius is 3r in this case.

P(You score at least 6 points) = area of circle with radius 3r / area of circle with radius 4r

P(You score at least 6 points) = π(3r)2 / π(4r)2

P(You score at least 6 points) = 9πr2 / 16πr2

P(You score at least 6 points) = 9 / 16 = 0.5625 or 56.25%

The probability that you score at least 6 points is 56.25%

2. P(You score exactly 3 points)

When you score exactly 3 points, you need to find the area outside the blue circle, but inside the black circle.

Let A be the area outside the blue circle, but inside the black circle.

A  = π(4r)2 - π(3r)2 = 16πr2 - 9πr2 = 7πr2

P(You score exactly 3 points) = A / area of circle with radius 4r

P(You score exactly 3 points) = 7π(r)2 / π(4r)2

P(You score exactly 3 points) = 7πr2 / 16πr2

P(You score exactly 3 points) = 7 / 16 = 0.4375 or 43.75%

The probability that you score exactly 3 points is 43.75%

3. P(You score at the most 6 points)

When you score at the most 6 points, your score is 3 points or 6 points. 

We already have an answer for scoring 3 points. It is 43.75%

We need to find P(You score exactly 6 points)

When you score exactly 6 points, you need to find the area outside the green circle, but inside the blue circle.

Let B be the area outside the green circle, but inside the blue circle.

B  = π(3r)2 - π(2r)2 = 9πr2 - 4πr2 = 5πr2

P(You score exactly 6 points) = B / area of circle with radius 4r

P(You score exactly 6 points) = 5π(r)2 / π(4r)2

P(You score exactly 6 points) = 5πr2 / 16πr2

P(You score exactly 6 points) = 5 / 16 = 0.3125 or 31.25%

The probability that you score exactly 6 points is 31.25%

4. P(The dart lands inside the red circle)

P(The dart lands inside the red circle) = area of circle with radius r / area of circle with radius 4r

P(The dart lands inside the red circle) = π (r)2 / π (4r)2

P(The dart lands inside the red circle) = πr2 / 16πr2

P(The dart lands inside the red circle) = 1 / 16 = 0.0625 or 6.25%

The probability that the dart lands inside the red circle is 6.25%