Find the perimeter in the coordinate plane

In order to find the perimeter in the coordinate plane, you can use the ruler postulate and the distance formula.

Example #1

Find the perimeter of triangle ABC in the figure below

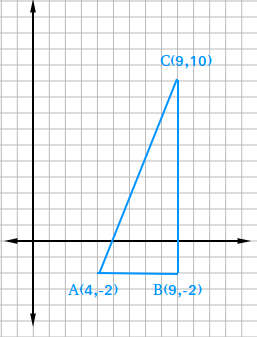
Find the length of each side of the triangle. Then, add the lengths to find the perimeter.

Using the ruler postulate, AB = |9 - 4| = |5| = 5

Using the ruler postulate, BC = |10 - -2| = |10 + 2| = |12| = 12

Using the distance formula, AC = √[(9 - 4)² + (10 - -2)²]

AC = √[(5)² + (10 + 2)²]

AC = √[(5)² + (12)²]

AC = √[25 + 144]

AC = √[169]

AC = 13

AB + BC + AC = 5 + 12 + 13 = 17 + 13 = 30

The perimeter of triangle ABC is 30 units.

Example #2

Find the perimeter of trapezoid ABCD in the figure below

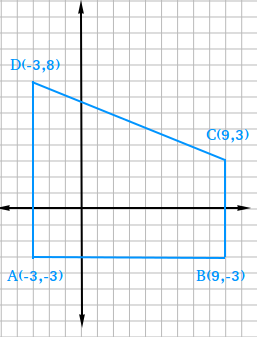
Find the length of each side of the trapezoid. Then, add the lengths to find the perimeter.

Using the ruler postulate, AB = |9 - -3| = |9 + 3| = |12| = 12

Using the ruler postulate, BC = |-3 - 3| = |-6| = 6

Using the ruler postulate, AD = |8 - -3| = |8 + 3| = |11| = 11

Using the distance formula, CD = √[(9 - -3)² + (3 - 8)²]

CD = √[(9 + 3)² + (-5)²]

CD = √[(12)² + 25]

CD = √[144 + 25]

CD = √[169]

CD = 13

AB + BC + AD + CD = 12 + 6 + 11 + 13 = 18 + 24 = 42

The perimeter of trapezoid ABCD is 42 units.