Finding the median
When finding the median of a set of data, first put the data in order and then find the number located right in the middle. The process is illustrated and summarized in the figure below.
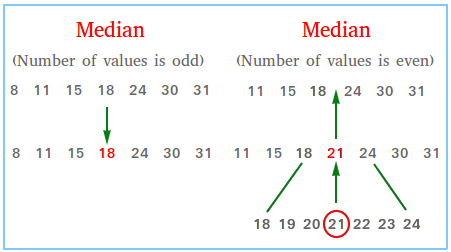
As you can see from the figure above, the median is 18 when the dataset is {8, 11, 15, 18, 24, 30, 31}.
The figure also shows that the median is 21 when the dataset is {11, 15, 18, 24, 30, 31}.
When the number of values is even, it may not be obvious to see the middle value. In this case, you can find the median by taking the average of the two numbers in the middle.
The two values in the middle for the dataset {11, 15, 18, 24, 30, 31} are 18 and 24.
Since (18 + 24) / 2 = 42 / 2 = 21, the median is 21.
More examples showing how to find the median when the number of values is odd
Example #1:
Find the median of the following set:
S1 = {15, 14, 11}
Put the numbers in the set in order
11, 14, 15
The median is 14 because it is in the middle.
Example #2:
Find the median of the following set:
S2 = {5, 3, 7, 2, 4}
Put the numbers in the set in order
2, 3, 4, 5, 7
In the example above, the median is 4 because 4 is in the middle.
When the number of numbers in the set is an odd number as in the two sets above, your median is right in the middle.
More examples showing how to find median when the number of values is even
Example #3:
Find the median of the following set:
S3 = {15, 14, 11,16}
Put S3 in order
11, 14, 15, 16
The two values in the middle are 14 and 15
The average is (14+15) / 2 = 29 / 2 = 14.5
So, the median is 14.5
Example #4:
Find the median of the following set:
S4 = {6, 2, 8, 9, 1, 10, 4, 12}
Tips when finding the median
When a set contains many numbers, cross out numbers as you put them in order to keep yourself organized.
For example for S4, put 1 in your new ordered list and then cross it out. Then, put 2 and cross it out...
Put S4 in order
1, 2, 4, 6, 8, 9, 10, 12
The two numbers in the middle are 6 and 8
(6 + 8) / 2 is 7, so the median is 7
When the number of numbers in the set is an even number, you will end up with two numbers in the middle. In this case, just take the average of the numbers.
Finding the median using the median formula
You can also find the median quickly using the median formula below.
Median = value of the [(n+1)/2]th term in a ranked data set with n equal to the number of values.
The lesson about median of a set of data will show you how.
Finding the median FAQs
-
The median of 4 and 7 is the value in the middle of 4 and 7. This value is between 5 and 6 as you can see in the list below.
4 5 6 7
Since 5.5 is the value between 5 and 6, the median of 4 and 7 is 5.5 -
If there are two numbers, just take the average of the two numbers to find the median.
-
From 1 to 10, the dataset is 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
The median is 5.5 or the value between 5 and 6.The median is the middle value of a set of numbers after the set has been ordered from least to greatest or from greatest to least.Suppose you have a list of numbers.
First, order the list.
Then, find the value in the middle of the list.
If there is an odd amount of numbers in the list, the median is the number in the middle of the list.
If there is an even amount of numbers in the list, the median is the average of the two numbers in the middle of the list.Unless you have only two values in the dataset, outliers have no effect on the median.
For example, suppose the dataset is 4, 6, 10, 200. Since you are using 6 and 10 to find the median, the outlier 200 has no effect.
Suppose the dataset has only two numbers such as 10, 200. Since you are using 10 and 200 to find the median, the outlier 200 will have an effect.
When looking for the average salary, statisticians prefer to find the median salary instead of using the mean. This ensures that those who are making millions do not skew or distort the data.