Fundamental Counting Principle
We will introduce the fundamental counting principle with an example. This counting principle is all about choices we might make given many possibilities.
Multiplication principle
Suppose most of your clothes are dirty and you are left with 2 pants and 3 shirts.
How many choices do you have or how many different ways can you dress?
Let's call the pants: pants #1 and pants #2
Let's call the shirts: shirt #1, shirt #2, and shirt #3
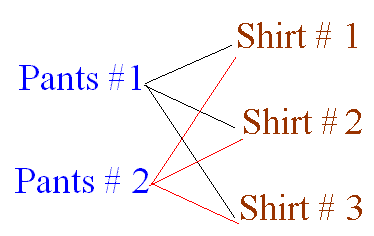
Then, a tree diagram as the one above can be used to show all the choices you can make.
As you can see on the diagram, you can wear pants #1 with shirt # 1. That's one of your choices.
Count all the branches to see how many choices you have.
Since you have six branches, you have 6 choices.
However, notice that a quick multiplication of 2 × 3 will yield the same answer.
In general, suppose you have n choices or n ways for a first task and m choices or m ways for a second task.
According to the multiplication principle, also called multiplication rule, you have n × m choices or n × m ways for both tasks.
In the example above, you have 2 choices for pants and 3 choices for shirts. Thus, you have 2 × 3 choices.
A couple more examples showing how to use the multiplication principle
Example #1:
You go a restaurant to get some breakfast. The menu says pancakes, waffles, or home fries. And for drink, coffee, juice, hot chocolate, and tea. How many different choices of food and drink do you have?
There 3 choices for food and 4 choices for drink.
Thus, you have a total of 3 × 4 = 12 choices.
Example #2:
You throw a die twice.
The first time you throw the die, the number of choices is n = 6.
The second time you throw the die, the number of choices is m = 6.
Thus, you have a total of m × n = 6 × 6 = 36 choices.
Addition principle
In the example above, you had to wear both a shirt and pants. In other situations, the choice is yours to do one or the other.
For example, suppose you go to a restaurant and there are 10 pork dishes and 15 lamb dishes. If you will either eat a pork dish or a lamb dish but not both, then you must use the addition principle.
How many different ways can you eat?
If you choose a pork dish, then you have 10 different choices
If you choose a lamb dish, then you have 15 different choices
The total number of ways you can eat is 10 + 15 = 25
In general, suppose you are dealing with disjoint events or events that cannot occur at the same time.
If have x choices or x ways for a first task and y choices or y ways for a second task.
According to the addition principle, also called rule of sum, you have x + y choices or x + y ways for both tasks.
Using both the multiplication principle and the addition principle
For example, suppose you go to a restaurant and there are 3 chicken dishes and 2 beef dishes. Your goal is to pick either a chicken dish or a beef dish. Then, for dessert, you will choose among 3 different flavors of ice-cream (vanilla, chocolate, and strawberry).
How many different ways you can eat?
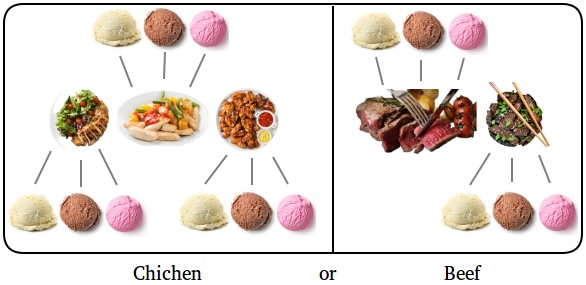
If you choose a chicken dish, then you have 3 choices for chicken and 3 choices for the ice-cream.
The number of choices for chicken and ice-cream is 3 × 3 = 9
If you choose a beef dish, then you have 2 choices for beef and 3 choices for the ice-cream.
The number of choices for beef and ice-cream is 2 × 3 = 6
The total number of choices is 3 × 3 + 2 × 3 = 9 + 6 = 15