Greatest common factor
The greatest common factor (GCF) is the largest factor of two numbers. An understanding of factor is important in order to understand the meaning of GCF.
What are factors?
When two or more numbers are multiplied in a multiplication problem, each number is a factor in the multiplication.
Take a look at the following multiplication problem:
2 × 8 × 3.
2 is a factor. 8 is also a factor.
How to find the factors of a number
You can find all factors of a number by finding all numbers that divide the number.
Find all factors of 36:
Start with 1. 1 divide 36, so 1 is a factor.
2 divides 36, so 2 is factor
3 divides 36, so 3 is a factor.
If you continue with this pattern, you will find that 1,2,3,4,6,9,12,18, and 36 are all factors of 36.
An easier way to handle the same problem is to do the following:
1 × 36 = 36
2 × 18 = 36
3 × 12 = 36
4 × 9 = 36
6 × 6 = 36
9 × 4 = 36.
Note that when the factors start to repeat, you have found them all.
In our example above, the factors started to repeat at 9 × 4 = 36 because you already has 4 × 9 = 36.
Therefore, we have found them all. If you need more practice on how to find the factors of a number, read the lesson about factors of 20.
You can also make a factor tree to find all the prime factors of a number
Now that you have understood how to get the factors of a number, it is going to be straightforward to to get the greatest common factor.
Whenever you are talking about greatest common factor, you are referring to 2, 3, or more numbers. Here, we will concern ourselves with just 2
The GCF of two numbers is the largest factor of the two numbers.
For instance, find GCF of 16 and 24 written as GCF(16,24).
How to find the greatest common factor
Method #1: Set intersection method:
First, list the factors of each number as a set.
The factors for 16 are 1, 2, 4, 8, and 16.
The factors for 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
Find the intersection of the two sets or simply the common factors.
The common factors are 1, 2, 4, and 8.
The largest factor for both numbers have in common is 8, so GCF(16,24) = 8.
Find GCF(7,12)
The factors for 7 are 1 and 7.
The factors for 12 are 1, 2, 3, 4, 6, and 12
The common factor is 1
The largest number both factors have in common is 1, so GCF(7,12) = 1
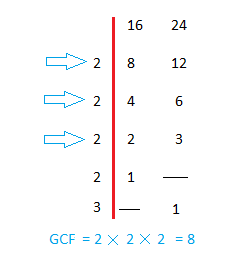
Method #2: My teacher's method: find gcf of 16 and 24
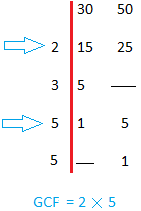
There is another example on the right to ensure that you understood this technique. GCF(30,50)
Technique:
Start by dividing each number by 2. (If 2 does not work, start with 3 instead, and so forth)
Keep dividing by 2 until 2 does not work anymore.
When 2 does not work anymore, divide by 3.
When 3 does not work anymore, divide by 4.
Keep doing this until you can no longer divide.
GCF(16,24) = 8
GCF(30,50) = 10
Method #3: Prime factorization method
Find GCF(24,36)
24 = 8 × 3 = 2 × 2 × 2 × 3 = 23 × 31
36 = 4 × 9 = 2 × 2 × 3 × 3 × 3 = 22 × 33
The greatest common factor will be 2x × 3y
x is the smaller exponent of 23 and 22
y is the smaller exponent of 31 and 33
The greatest common factor is 22 × 31 = 2 × 2 × 3 = 12