How to do synthetic division
This lesson will explain how to do synthetic division to quickly divide a polynomial by another.
A couple of synthetic division examples are shown below.
The quotient is x + 6
Explanation of the steps we took while using synthetic division to divide x2 + 11x + 30 by x + 5.
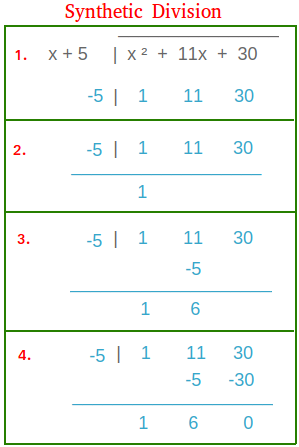
1.
Reverse the sign of the constant term in the divisor. For example, the constant term in the divisor is 5. Change it to -5. Remove the coefficients from the dividend and rewrite the division as shown above in blue.
2.
Bring down the first coefficient or 1. The 1 will begin the quotient.
3.
Multiply the first coefficient by the new divisor and add the answer to the next coefficient or 11. We get 6. write down 6 in the same position as 11 and -5.
4.
Keep multiplying and adding until the remainder is found. For example, multiply 6 by -5. We get -30. Add -30 to 30 to get 0 and 0 is the remainder. In fact, the last number on the right that you find after you add is the remainder whether it is 0 or not.
How to do synthetic division when the degree of the polynomial is 3
Divide x3 + 5x2 -2x - 24 by x - 2
Step 1: Reverse the sign of the constant term in the divisor. In other words, change -2 in x - 2 into 2 and bring it down.
_____________________
x - 2 | x ³ + 5x² - 2x - 24
2 | 1 5 -2 -24
Step 2: Bring down the first coefficient or 1. The 1 will begin the quotient.
2 | 1 5 -2 -24
________________________
1
Step 3: Multiply 1 by 2 and add the result to 5. The result is 7. Bring 7 down.
2 | 1 5 -2 -24
2
________________________
1 7
Step 4: Multiply 7 by 2 and add the result to -2. Keep multiplying and adding until the remainder is found.
2 | 1 5 -2 -24
2 14
__________________________
1 7 12
2 | 1 5 -2 -24
2 14 24
__________________________
1 7 12 0
The quotient is x² + 7x + 12
Synthetic division is also called the method of detached coefficients. This is because the first step in synthetic division is to remove the coefficients from the polynomial that is being divided.