Length of a ladder and the Pythagorean theorem

by Anonymous

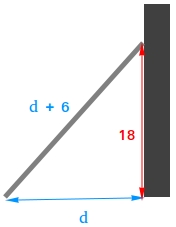
A ladder is resting against a wall. The top of the ladder touches the wall at a height of 18 ft. Find the length of the ladder if the length is 6 ft more than its distance from the wall.

Let d be the distance from the wall, then d + 6 is the length of the ladder as shown in the picture above.

Using the Pythagorean theorem, we get:

(d + 6)² = d² + 18²

d² + 12d + 36 = d² + 18²

12d + 36 = 324

12d = 324 - 36

12d = 288

d = 288/12

d = 24

Since d + 6 = 24 + 6 = 30, the length of the ladder is 30.