Multiplication by 11
In order to understand the multiplication by 11 trick,take a look at the following multiplication below: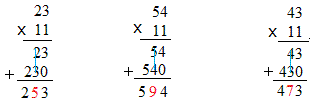
For example, when you multiply 23 by 11, 2 and 3 appear again in the answer. By the same token when you multiply 54 by 11, 5 and 4 appear in the answer.
Second, the number in the middle of the answer is always found by adding the digits of the number that is multiplied by 11.
For example, when multiplying 23 by 11, just add 2 and 3 to get 5 and put 5 between 2 and 3. The answer is 253. By the same token, when multiplying 54 by 11, just add 5 and 4 to get 9 and put 9 between 5 and 4. The answer is 594.
This is the basic facts that you have to remember to quickly multiply numbers by 11.
Therefore, if you want to use this trick, all you have to do is add the digits of the number you are multiplying by 11 and put the answer between these digits.
Other examples showing how to do multiplication by 11
1) 35 × 11
Just add 3 and 5 to get 8
Put 8 between 3 and 5
The answer is 385
2) 18 × 11
Just add 1 and 8 to get 9
Put 9 between 1 and 8
The answer is 198
3) 43 × 11
Just add 4 and 3 to get 7
Put 7 between 4 and 3
The answer is 473
Now, look at this example 48 × 11
Add 4 and 8 to get 12
Just put 12 between 4 and 8???
No, it does not work like this!
You can still put 2 in between. However, since the number is bigger than 9, you have to carry the 10 represented with a 1 over the 4.
1 + 4 = 5. Thus the answer is 528
4) 85 × 11
Just add 8 and 5 to get 13
Add 1 to 8 to get 9
Put 3 between 9 and 5
The answer is 935
5) 78 × 11
Just add 7 and 8 to get 15
Add 1 to 7 to get 8
Put 5 between 8 and 8
The answer is 858