Multiplication of binomials geometrically
In this lesson, we will perform the multiplication of binomials geometrically. In other words, we will use area models to do the multiplication.
Example #1
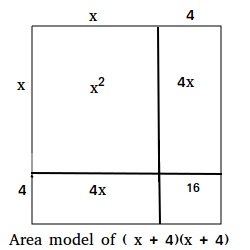
Consider the product (x + 4)2
(x + 4)2 = (x + 4)(x + 4). The area model is shown in the figure below.
The area we are looking for is that of the entire square, which is the sum of the four inner regions.
(x + 4)2 = x2 + 4x + 4x + 16
(x + 4)2 = x2 + 8x + 16
Example #2
Consider the product (x + 3)(x + 2). This is very similar to example #1.
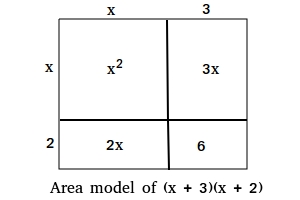
The area we are looking for is that of the preceding entire rectangle, which is the sum of the four inner regions.
(x + 3)(x + 2) = x2 + 3x + 2x + 6
(x + 3)(x + 2) = x2 + 5x + 6
Two more interesting examples showing how to do multiplication of binomials geometrically
Example #3
Consider the product (x + 4)(x - 2)

Notice that the area we are looking for this time though cannot be found by adding the sum of the four inner regions. Only the top two rectangles will give us the area that we are looking since they are the ones that model (x + 4)(x - 2)
(x + 4)(x - 2) = x(x - 2) + 4(x - 2)
(x + 4)(x - 2) = x2 -2x + 4x - 8
(x + 4)(x - 2) = x2 + 2x - 8
Example #4
Consider the product (x - 4)(x - 2)
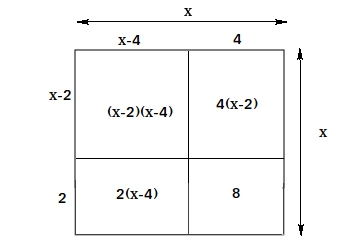
The area we are looking for cannot be found by using the upper left rectangle which is a representation of (x-4))(x-2). To find the area we need to find the area of the large square and then subtract the areas of the other three rectangles from it.
(x - 4)(x - 2) = x2 - 4(x - 2) - 2(x - 4) - 8
(x - 4)(x - 2) = x2 - 4x + 8 - 2x + 8 - 8
(x - 4)(x - 2) = x2 - 4x + 8 - 2x
(x - 4)(x - 2) = x2 - 6x + 8