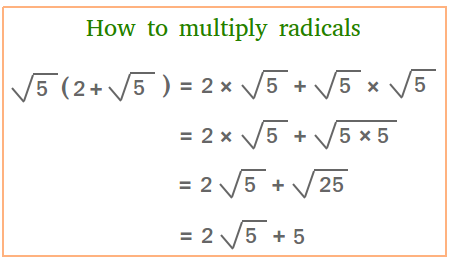Multiplication of radicals using the distributive property
Learn how to perform multiplication of radicals with some carefully chosen examples using the distributive property.
Examples showing how to do multiplication of radicals
Example #1
|
$$
(\sqrt{3} + \sqrt{2}) × (\sqrt{3} - \sqrt{2}) $$
|
|
Here is how you can use the distributive property to do this multiplication.
|
$$
(\sqrt{3} + \sqrt{2}) × (\sqrt{3} - \sqrt{2}) $$
|
|
|
$$ =
\sqrt{3}×\sqrt{3} - \sqrt{3}×\sqrt{2} + \sqrt{2}×\sqrt{3} - \sqrt{2}×\sqrt{2} $$
|
|
|
$$ =
\sqrt{3}×\sqrt{3} - \sqrt{3}×\sqrt{2} + \sqrt{2}×\sqrt{3} $$
|
|
|
$$
- \sqrt{2}×\sqrt{2} $$
|
|
|
$$ =
\sqrt{3 × 3} - \sqrt{3 × 2} + \sqrt{2 × 3} - \sqrt{2 × 2} $$
|
|
|
$$ =
\sqrt{9} - \sqrt{6} + \sqrt{6} - \sqrt{4} $$
|
|
|
$$ =
\sqrt{9} - \sqrt{4} $$
|
|
= 3 - 2
= 1
Did you notice that the multiplication has the format (a + b) x (a - b)?
(a + b) x (a - b) = a2 - b2
Therefore, next time, there is absolutely no need to do at all this math above.
|
$$
(\sqrt{3} + \sqrt{2}) × (\sqrt{3} - \sqrt{2}) = (\sqrt{3})^2 -
(\sqrt{2})^2 $$
|
|
|
$$
Notice \ that (\sqrt{3})^2 = 3 $$
|
|
$$
Notice \ also \ that (\sqrt{2})^2 = 2 $$
|
$$
In \ general,\sqrt{a} ×\sqrt{a} = (\sqrt{a})^2 = a $$
|
|
Example #2
|
$$
(\sqrt{7} + \sqrt{5}) × (\sqrt{7} - \sqrt{5}) $$
|
|
Once again, notice that the multiplication has the format (a + b) x (a - b).
Therefore, you can just use the formula below to quickly get an answer:
(a + b) x (a - b) = a2 - b2
|
$$
(\sqrt{7} + \sqrt{5}) × (\sqrt{7} - \sqrt{5}) $$
|
|
|
$$
= (\sqrt{7})^2 -
(\sqrt{5})^2 = 7 - 5 = 2 $$
|
|
Example #3
|
$$
(\sqrt{6} + \sqrt{9}) × (\sqrt{6} - \sqrt{9}) = 6 - 9 = -3 $$
|
|
Example #4
|
$$
(\sqrt{4} - 2\sqrt{12}) × (\sqrt{4} + \sqrt{12}) $$
|
|
|
$$ =
\sqrt{4} × \sqrt{4} + \sqrt{4} × \sqrt{12} -2\sqrt{12} ×\sqrt{4} -2 \sqrt{12} × \sqrt{12} $$
|
|
|
$$ =
(\sqrt{4} × \sqrt{4} + \sqrt{4} × \sqrt{12} -2\sqrt{12} ×\sqrt{4} $$
|
|
|
$$ -2 \sqrt{12} × \sqrt{12} $$
|
|
|
$$ =
4 + 2 × \sqrt{12} -2\sqrt{12} ×2 -2 × 12 $$
|
|
|
$$ =
4 + 2\sqrt{12} -4\sqrt{12} -24 $$
|
|
Study also the example in the figure below carefully if you did not quite understand the ones above or need more examples to master the topic.