How to multiply matrices

Before I show you how to multiply matrices, let's see how to multiply a matrix by a scalar or a real number.

For example, to multiply 4 by a 2x2 matrix, just multiply 4 by every element in the matrix.

This technique works well if you don't want to write down the matrix 4 times.



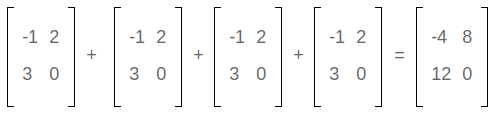
Instead of writing down the matrix above 4 times, it is better to multiply every number in the matrix below by 4.

-1	2
3	0

After multiplication, we get the following matrix:

-4 8 12 0

This will work with any matrix. It does not matter what the dimension is, just multiply the scalar by every element in the matrix.

Now here is the technique to multiply matrices.

Multiply the elements of each row of the first matrix by the elements of each column of the second matrix. Then, add the products.

Does it make sense? Probably not! Let's illustrate how to multiply matrices with a 2x2 matrix. Once you understand how to do multiplication with a 2x2 matrix, you can do it with matrices of any dimension.

First example showing how to multiply matrices

If you did not understand the example above, keep reading as we break the multiplication down into more manageable steps.

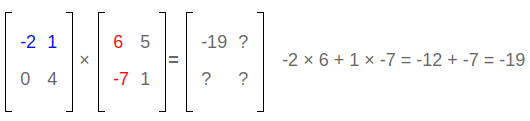
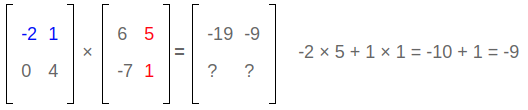
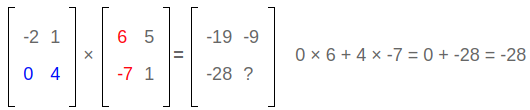
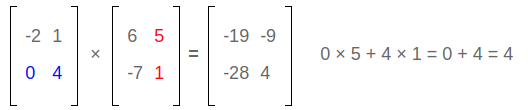
Observation #1:

Did you notice this pattern to follow when you multiply matrices?

row #1 × column #1: answer goes in row #1 column #1.

row #1 × column #2: answer goes in row #1 column #2.

row #2 × column #1: answer goes in row #2 column #1.

row #2 × column #2: answer goes in row #2 column #2.

Observation #2:

Matrix on the left (call it matrix A): number of elements in first row determine the number of columns.

Matrix on the right (call it matrix B): number of elements in first column determine the number of rows.

Since you are multiplying every element in first row by every element in first column, multiplication will not be possible if the number of columns of matrix A is not equal to the number of rows of matrix B.

The following multiplication is therefore not possible. Call the matrix on the left A and the matrix on the right B.

-2 0

×

6 5 -7 1

After you multiply -2 by 6, you got no number to multiply 7 by. It does not work as already stated because the number of columns of matrix A is not equal to the number of rows of matrix B.

The product of 2 matrices A and B exists only if the number of columns of A is equal to the number of rows of B.

For example, the following matrices can be multiplied. See in green how the number of columns is equal to the number of rows.

2x2 and 2x3
3x1 and 1x4
4x3 and 3x1
2x5 and 5x2
1x3 and 3x1

The following matrices cannot be multiplied. See in red that the number of columns of matrix A is not equal to the number of rows of matrix B.

2x2 and 3x3
3x2 and 1x4
4x3 and 2x2
2x5 and 2x5
1x3 and 1x5

Dimensions of a product matrix

It is easy to find the dimension of a matrix. Let's take a look again at the matrices below we said could be multiplied.

2x2 and 2x3. Dimension is 2x3
3x1 and 1x4. Dimension is 3x4
4x3 and 3x1. Dimension is 4x1
2x5 and 5x2. Dimension is 2x2
1x3 and 3x1. Dimension is 1x1

How did we get the dimension?

The number of rows of the product matrix is the number of rows of the matrix on the left.

The number of columns of the product matrix is the number of columns of the matrix on the right.

Second example showing how to multiply matrices

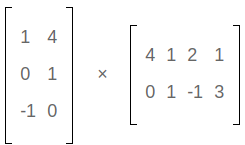
Call the matrix on the left A and the matrix on the right B. Looking at A and B, we can confidently say a couple of things.

The dimensions of A is 3x2 and the dimensions of B is 2x4.

This means that we can find the product and the dimension of the product is 3x4.

There will be 12 multiplications


First row times first column: 1 × 4 + 4 × 0 = 4 + 0 = 4

First row times second column: 1 × 1 + 4 × 1 = 1 + 4 = 5

First row times third column: 1 × 2 + 4 × -1 = 2 + -4 = -2

First row times fourth column: 1 × 1 + 4 × 3 = 1 + 12 = 13



Second row times first column: 0 × 4 + 1 × 0 = 0 + 0 = 0

Second row times second column: 0 × 1 + 1 × 1 = 0 + 1 = 1

Second row times third column: 0 × 2 + 1 × -1 = 0 + -1 = -1

Seecond row times fourth column: 0 × 1 + 1 × 3 = 0 + 3 = 3



Third row times first column: -1 × 4 + 0 × 0 = -4 + 0 = -4

Third row times second column: -1 × 1 + 0 × 1 = -1 + 0 = -1

Third row times third column: -1 × 2 + 0 × -1 = -2 + 0 = -2

Third row times fourth column: -1 × 1 + 0 × 3 = -1 + 0 = -1

The result is shown below:

4 5 -2 13 0 1 -1 3 4 -1 -2 -1

Multiply matrices quiz. Check you understanding of this lesson.