Definition and equation of a parabola
By definition, a parabola is the set of all points (x,y) in a plane that are the same distance from a fixed line and a fixed point not on the line. The fixed point is the focus and the fixed line is the directrix.
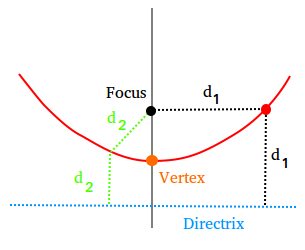
Take a look at the figure below and make note of the following important observations.
The focus is the distance from the orange dot (vertex) to the black dot.
The distance from the focus ( black dot ) to the point on the parabola ( red dot ) is the same as the distance from the point on the parabola ( red dot ) to the directrix. We use the symbol d1 for both distances to show that the distance is the same.
By the same token,
d2 is the distance from the focus to a point on the line
d2 is also the distance from the point on the line to the directrix
d2 = d2
Finally, notice that the distance from the focus to the vertex is equal to the distance from the vertex to the directrix.
Using the definition of a parabola to find the equation of a parabola.
Write an equation for a graph that is the set of all points in the plane that are at the same distance from the point (0,4) and the line y = -4
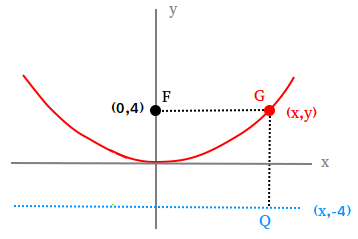
According to the definition, FG = GQ. Therefore, let us find all points P(x,y) such that FG and the distance from G to the line are equal.
Now set FG = GQ
Raise both sides to the second power.
x2 + (y - 4)2 = (y + 4)2
x2 + y2 - 8y + 16 = y2 + 8y + 16
x2 - 8y + 16 = 8y + 16 ( Cancel y2 )
x2 - 8y = 8y ( Cancel 16 )
x2 = 8y + 8y
x2 = 16y ( equation of a parabola )
y = x2 / 16
How to derive the standard equation of a parabola when its vertex is at the origin
In the previous section, the equation of the parabola of all points in the plane that are at the same distance from the point (0,4) and the line y = -4 was x2 = 16y. Furthermore, the vertex of the parabola was at the origin.
The equation x2 = 16y is in standard form. We can again use the definition of a parabola to find the standard form of the equation of a parabola with its vertex at the origin. Place the focus at the point (0, p). Then, the directrix has an equation given by y = -p.
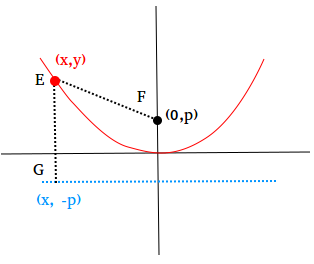
The point (x,y) is on the parabola if and only if EF = EG
Set EF equal to EG
Raise both sides to the second power
x2 + (y - p)2 = (y + p)2
x2 + y2 - 2yp + p2 = y2 + 2yp + p2
x2 - 2yp = 2yp ( Cancel y2 and p2)
x2 - 2yp + 2yp = 2yp + 2yp
x2 = 4yp ( Equation of a parabola that open upward or downward.)
Similarly, we can derive the equation of a parabola with its vertex at the origin. This time though we place the focus at the point ( p, 0). Then, the directrix has an equation given by x = -p.
The equation is y2 = 4xp ( Equation of a parabola that open to the right or to the left)
How to derive the standard equation of a parabola when its vertex is located at (h,k)
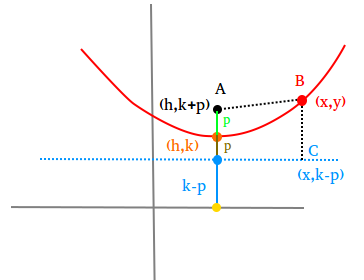
The graph above shows a parabola whose vertex is the orange dot located at (h,k). Recall that p is the distance from the vertex to the focus. Therefore k + p is the y-coordinate of the black dot or the focus.
The y-coordinate of the dashed blue line or directrix is k-p. Why ?
Let s be the distance from the yellow dot to the blue dot.
Let p be the distance from the blue dot to the orange dot.
We know that k is the distance from yellow dot to the orange dot.
k = s + p
s = k - p
According to the definition, AB = BC
Now set AB = BC
= y - (k-p)
Raise both sides to the second power
(x - h)2 + [y - (k+p)]2 = [y - (k-p)]2
(x - h)2 + y2 -2y(k+p) + (k+p)2 = y2 -2y(k-p) + (k-p)2
(x - h)2 -2y(k+p) + (k+p)2 = -2y(k-p) + (k-p)2
(x - h)2 -2yk - 2yp + k2 + 2pk + p2 = -2yk + 2yp + k2 -2pk + p2
(x - h)2 - 2yp + k2 + 2pk + p2 = 2yp + k2 -2pk + p2
(x - h)2 - 2yp + k2 + 2pk = 2yp + k2 -2pk
(x - h)2 - 2yp + 2pk = 2yp -2pk
(x - h)2 = 4yp - 4pk
(x - h)2 = 4p(y - k)
The equation (x - h)2 = 4p(y - k) above applies when the parabola opens upward or downward with a directrix of y = k-p
If the parabola opens to the right or to the left with a directrix of x = h-p,
the equation to use is (y - k)2 = 4p(x - h)
Now let us practice.
Example #1:
Find the standard form of the equation of a parabola with vertex (3, 1) and focus (3, 6)
Solution
First, notice that when you connect the vertex and the focus, they form a vertical line.This means that the parabola either opens upward or downward.
Therefore, the equation to use is (x - h)2 = 4p(y - k)
Remember that (h, k) is the coordinate of the vertex. So (h, k) = (3, 1)
y = k + p is the y-coordinate of the focus
p = y - k = 6 - 1 = 5
The standard form is (x - 3)2 = 4 × 5 (y - 1) = (x - 3)2 = 20(y - 1)