Parallel circuit rules

The parallel circuit rules show how to use Ohm's law when the circuit has more than one device receiving electrical energy. The rules will also help us see how the resistance, the current, and the voltage change in the parallel circuit. 

Below is an example of a parallel circuit with 5 electrical components, excluding wires. The circuit has 2 switches (green), 1 voltage source of 24 volts, and 2 resistors. 

To be more precise, the circuit below has 2 pathways.

Simply put, the current has the ability to "make choices" as to where it would go. If the current can either go this way or that way, then the circuit is a parallel circuit. A circuit where electrons that cannot "make choices" as to how they will flow is a series connection.

Look carefully at the circuit below and you will see that the current can either go to the 8 Ohms resistor or the 4 Ohms resistor. This is what we mean by "making choices."

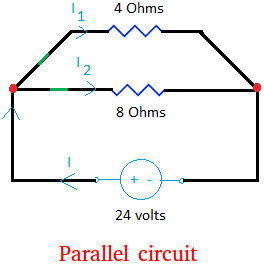
Take a close look at the two red dots. Did you notice that both resistors are connected to the same two red dots? This means that both resistors are fed by the same voltage of 24 volts. 

Let V be the voltage feeding the circuit

Let V₁ be the voltage feeding the device with the 4 Ohms resistor.

Let V₂ be the voltage feeding the device with 8 Ohms resistor.

Then, V = V₁ = V₂

Now, let us talk about the current. Let us pretend that the resistance is the same in both branches as shown in the circuit diagram below.

Since there is a resistance, the current going there will be less.

Since the resistance is the same for both branches, it makes sense to say that both branches will receive the same amount of current.

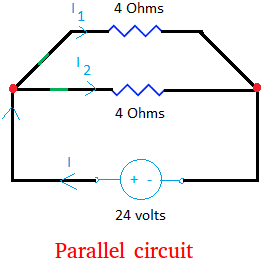
The total current I is split into I₁ and I₂. Half of the current will go to the branch with the 4 Ohms resistor and the other half to the branch with the 4 Ohms resistor.

If one resistor is equal to 4 Ohms and the other 8 Ohms like the first figure, more current will go to the branch with 4 Ohms. In fact twice as much current will go to the branch with a lesser resistance.

However, the amount of current that will go to the two branches must equal the amount that came from the source or the current I.

I = I₁ + I₂

Now we can find the resistance for the circuit using I = I₁ + I₂

Let R₁ and R₂ be the resistances in the 2 branches. Let R_p be the resistance of the circuit. The resistance of the circuit is usually called equivalent resistance or total resistance. Ohm's law will apply separately to each branch.

I = I₁ + I₂

V/R_p = V/R₁ + V/R₂

V/R_p = V(1/R₁ + 1/R₂)

Divide both sides of the equation by V and you will end up with Rule #3

Parallel circuit rules generalization

The parallel circuit rules can be summarized and generalized as  shown below.

Let V be the voltage feeding the circuit

Let V₁, V₂,..., V_n be the voltage feeding other devices in the branches

Then, V = V₁ = V₂ = ... = V_n

Let I be the current in the circuit

Let I₁, I₂,..., I_n be the current going to other devices in the branches

Then, I = I₁ + I₂ + ... + I_n

Let R₁, R₂, ... , R_n be the resistances in the branches. Let R_p be the equivalent resistance.

1 / Rp

=   1 / R1

+   1 / R2 + ...

+   1 / Rn

Any questions about the parallel circuit rules? Send an email

Parallel circuit rules quiz

Take the parallel circuits quiz below to see how well you understand parallel circuits. After completing this quiz with 100% accuracy, you will know exactly how the current, the voltage, and the resistors behave in a parallel circuit. You will not need to use a paper and pencil to complete this quiz.

First, read the lesson about parallel circuits and then take this quiz.

Objective of the parallel circuit quiz:

• Know how the current behaves in a parallel circuit
• Know how the voltage behaves in a parallel circuit
• Know how the resistor behaves in a parallel circuit
• Know how to apply Ohm's law to find the current going through the circuit.
• Find the current in the circuit