Preschool math worksheets

Find here a variety of free printable preschool math worksheets. These worksheets will help kids to get ready for math taught in kindergarten.

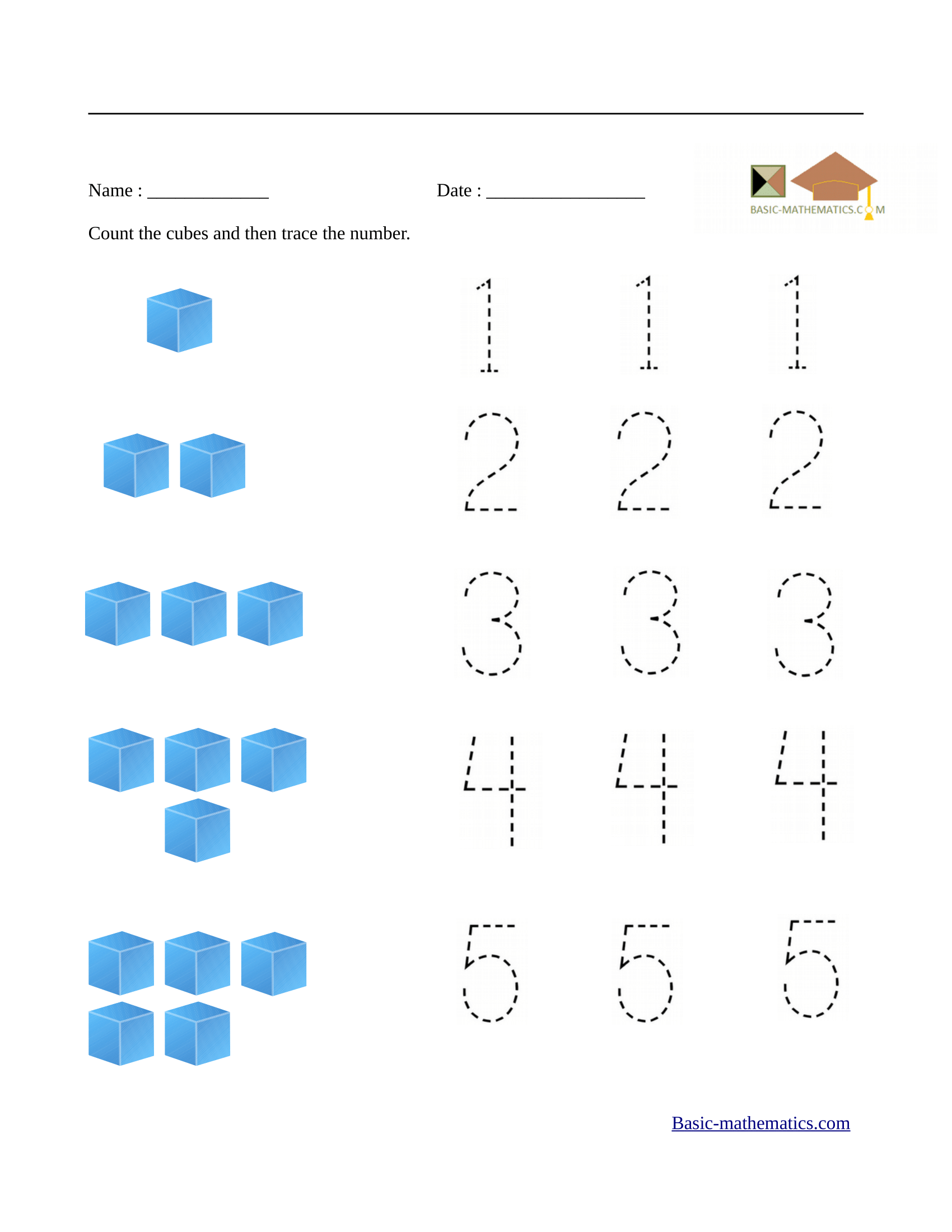
The two worksheets below will teach preschool students how to count or find the number of items in a set.  Then, they can recognize the number assigned to the number of items and finally trace that number. Tracing numbers will help young children boost fine motor skills.

First, count the cubes and then trace the number associated with the number of cubes. Count and trace numbers worksheet 1 Numbers from 1 to 5

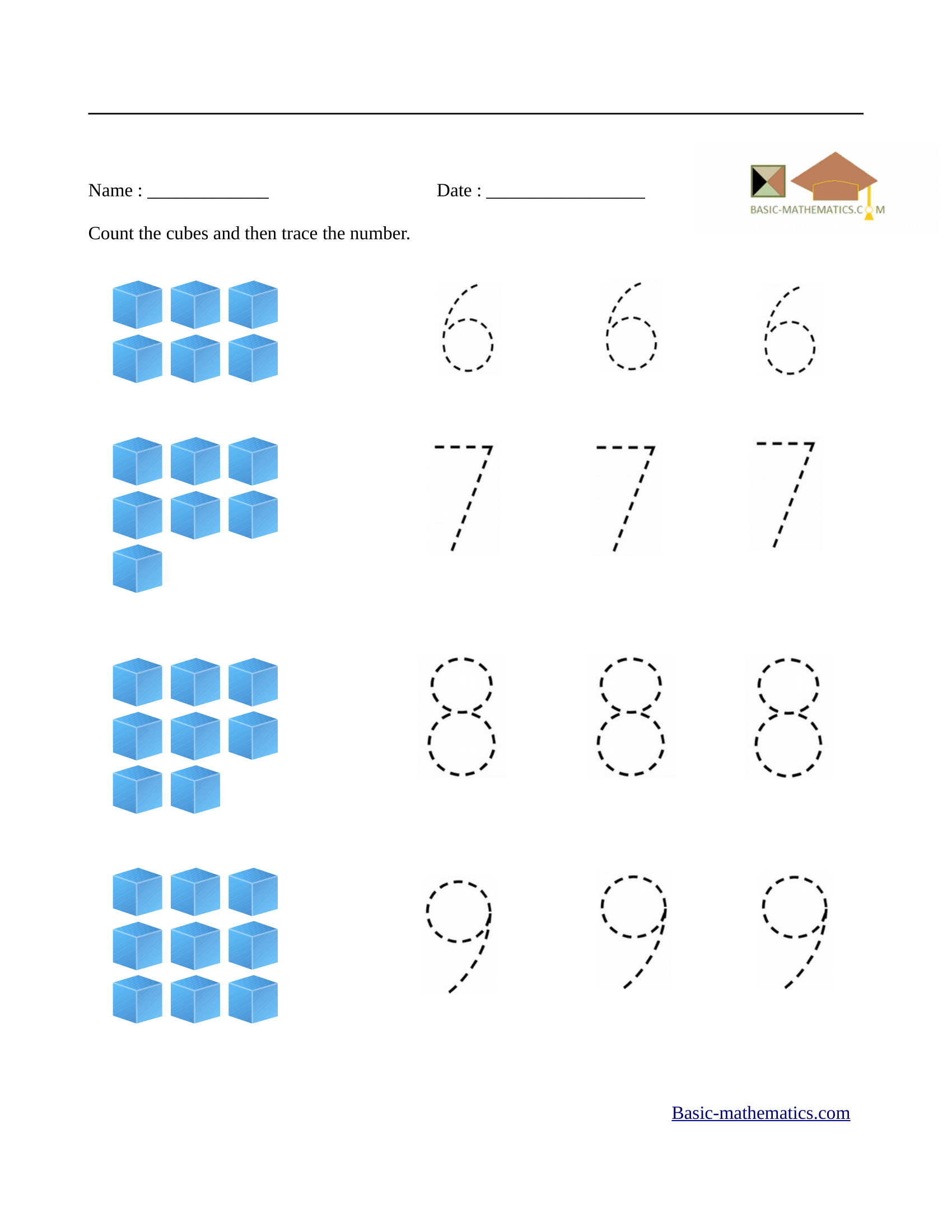
Count and trace numbers worksheet 2 Numbers from 6 to 9

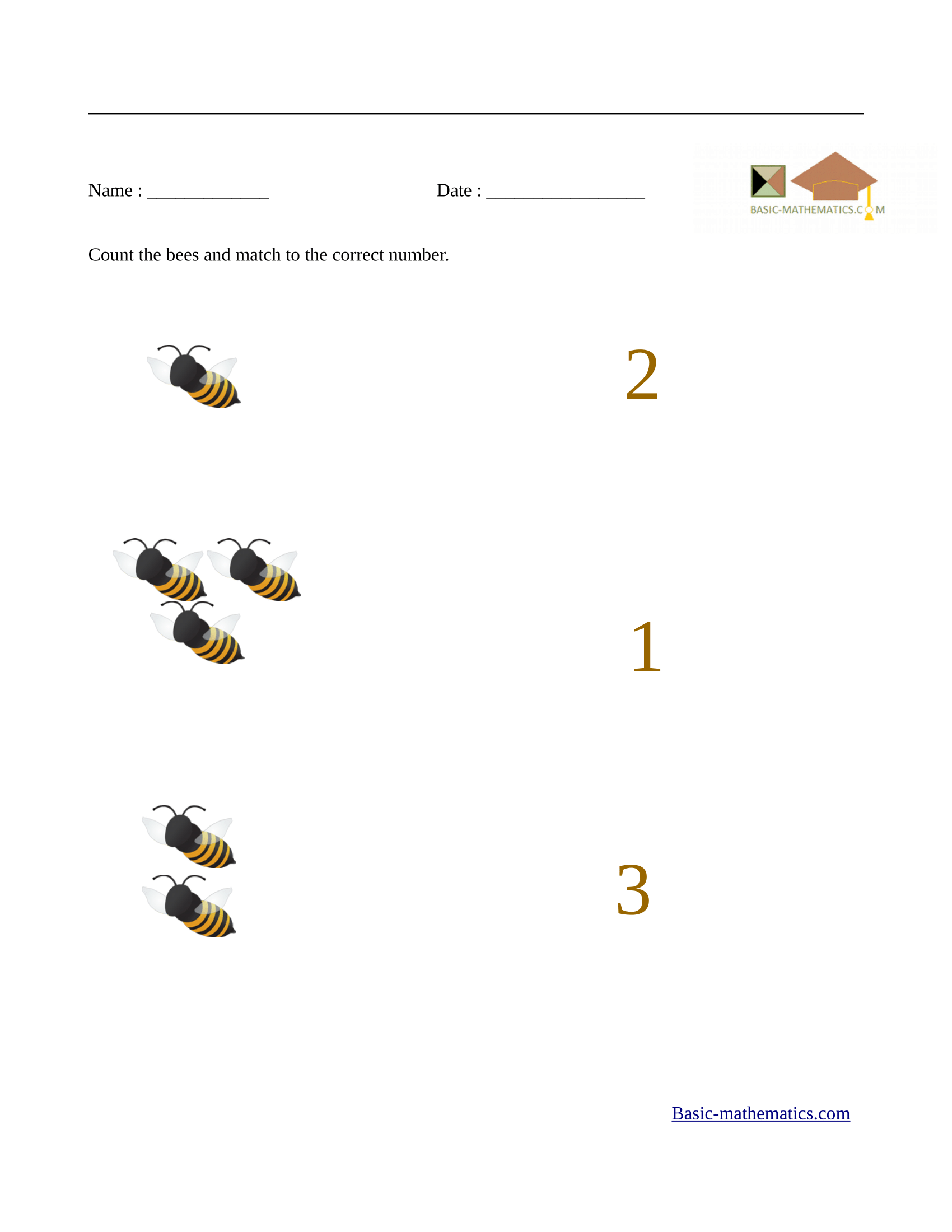
The two worksheets below will teach students how to count or find the number of items in a set.  Then, they can try to match the number of items to the correct number on the right.

First count the bees. Then match the number of bees to the corresponding number on the right. Count and match worksheet 1

Count the bees and match the number of bees to the corresponding number word. Count and match worksheet 2

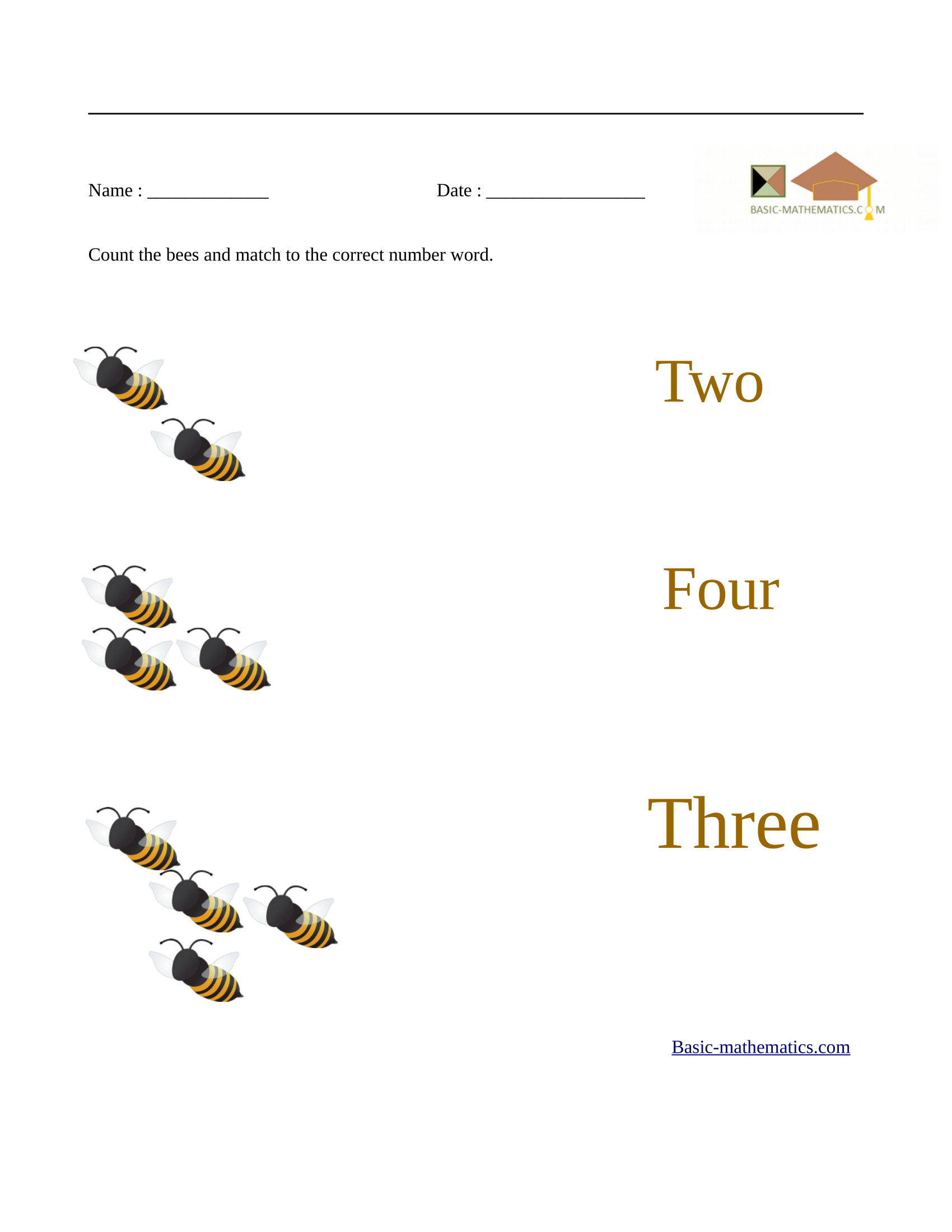
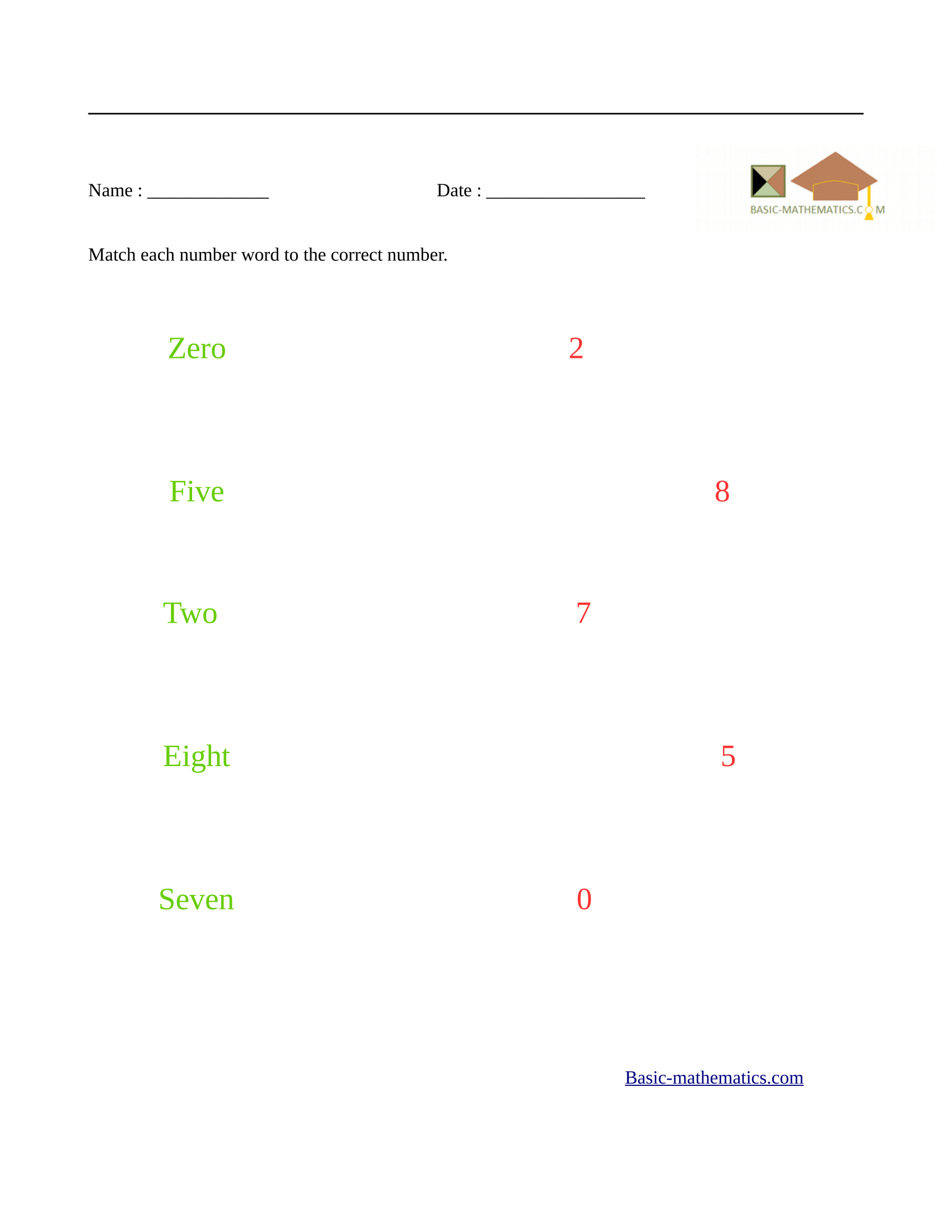
The two worksheets below will teach students to match a number word to the correct number.

Number words worksheet 1

Number words worksheet 2

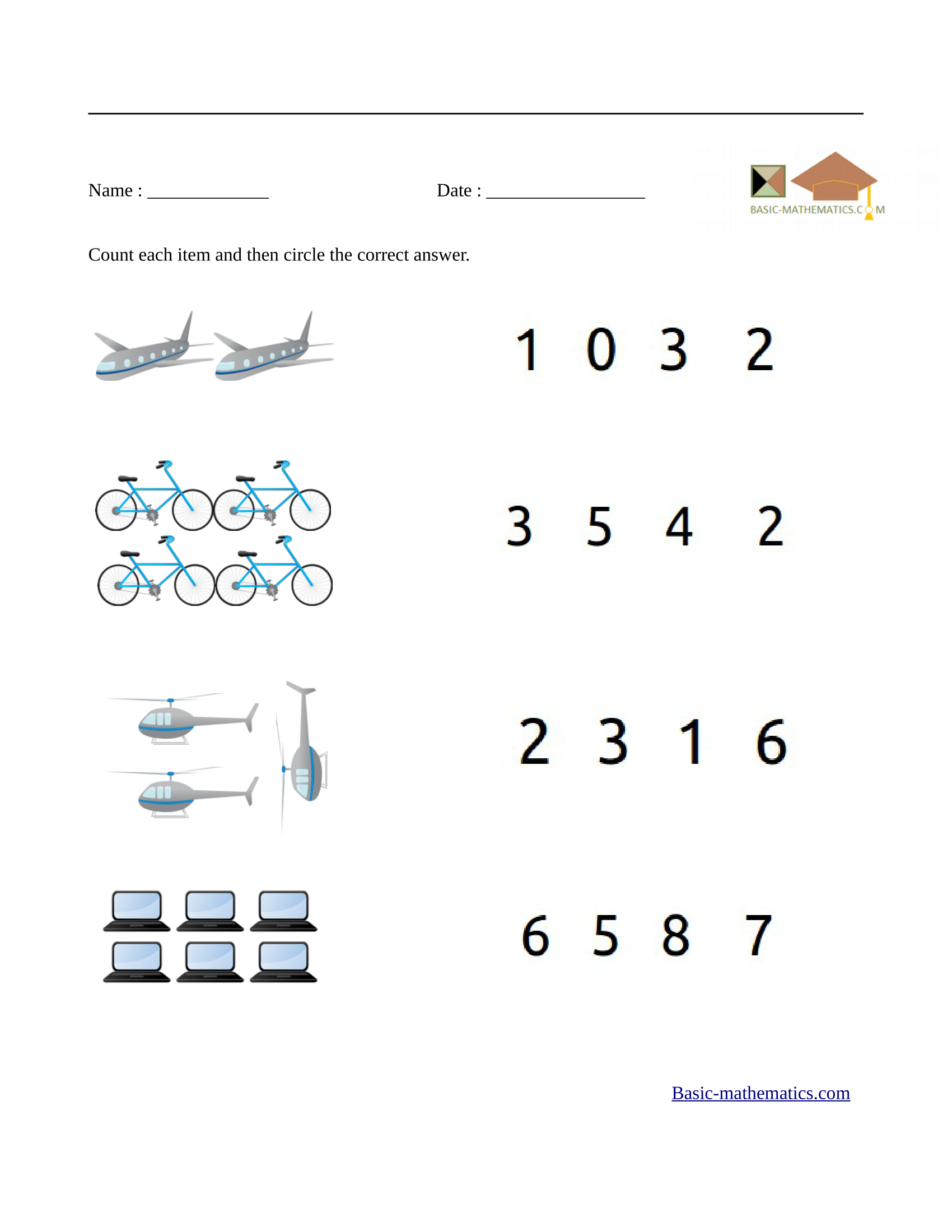
The worksheet below will allow students to count each item and then choose the correct answer from a list of answers.

Count each item worksheet