Prime Number
A prime number is a number that is divisible only by 1 and itself. A number is divisible by another number when the remainder is zero.
For example, 7 is a prime number because 7 is only divisible by 1 and 7. This means that if you divide 7 by a number that is not 1 or 7, you will not get a remainder of zero.
7 divided by 1 gives a remainder of 0 since 7 = 1 × 7 + 0
7 divided by 2 gives a remainder of 1 since 7 = 2 × 3 + 1
7 divided by 3 gives a remainder of 1 since 7 = 3 × 2 + 1
7 divided by 4 gives a remainder of 3 since 7 = 4 × 1 + 3
7 divided by 5 gives a remainder of 2 since 7 = 5 × 1 + 2
7 divided by 6 gives a remainder of 1 since 7 = 6 × 1 + 1
7 divided by 7 gives a remainder of 0 since 7 = 7 × 1 + 0
As illustrated above, only when 7 is divided by 1 and 7 will you get a remainder of zero. We can also say that the only factors of 7 are 1 and 7. This gives us a second way to define a prime number.
Definition #2: A number is prime if the number has only 2 factors, 1 and itself.
If the number has more than two factors, we say that the number is composite.
For instance, 12 is a composite number because 12 has more than 2 factors. It can be divided by numbers other than 1 and 12, such as 2, 3, and 4 which can also be called factors.
A few interesting facts about prime numbers
- 1 is neither prime nor composite because it has only one factor. According to the definition, a number must have at least 2 factors before it can be prime or composite.
- Notice also that 2 is the only number that is even and prime at the same time.
- There are 15 prime numbers less than 50.
- There are 25 prime numbers less than 100. Can you find them?
You can use the definition to test every single number. However, it is somewhat time-consuming.
As a shortcut, you can use a method or algorithm called Sieve of Eratosthenes, named after a famous Greek mathematician.
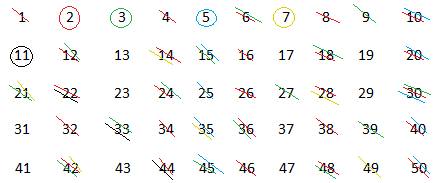
Using Sieve's algorithm to find prime numbers between 1 and 50.
- Make a list of all numbers from 1 to 50.
- Start by crossing out 1 because it is not prime. Then, circle the next number after 1 that is prime, which is 2.
- Cross out all the multiples of 2 until you get to 50, such as 2, 6, 8, 10, 12...
- Look for the next number after 2 that is prime. That number is 3. Circle 3 and cross out all multiples of 3, such as 6, 9, 12, ...
- Repeat the process with 5 and 7, etc. After you are done, you should find 25 prime numbers.
We show you the process for all numbers from 1 to 50.
The numbers that are circled and not crossed out are the prime numbers. There are 15 prime numbers between 1 and 50.
Important observation:
The number 30 is crossed out by a blue, a red, and a green line. This means that 30 can be divided by 2, 3 and 5.
Therefore, the prime numbers less than 50 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, and 47.