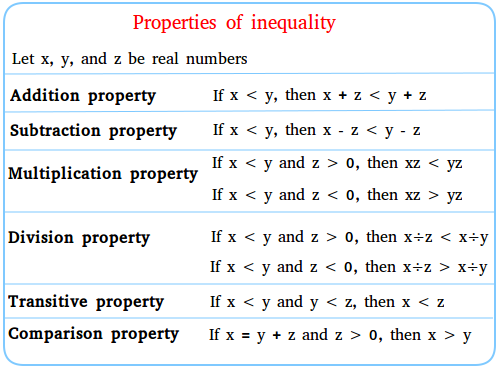
Properties of inequality
We will show 6 properties of inequality. When appropriate, we will illustrate with real life examples of properties of inequality.Addition property:
If x < y, then x + z < y + z
Example: Suppose Sylvia's weight < Jennifer's weight, then Sylvia's weight + 4 < Jennifer's weight + 4
Or suppose 1 < 4, then 1 + 6 < 4 + 6
If x > y, then x + z > y + z
Example: Suppose Sylvia's weight > Jennifer's weight, then Sylvia's weight + 9 > Jennifer's weight + 9
Or suppose 4 > 2, then 4 + 5 > 2 + 5
Subtraction property:
If x < y, then x − z < y − z
Example: Suppose Sylvia's weight < Jennifer's weight, then Sylvia's weight − 4 < Jennifer's weight − 4
Or suppose 4 < 8, then 4 − 3 < 8 − 3
If x > y, then x − z > y − z
Example: Suppose Sylvia's weight > Jennifer's weight, then Sylvia's weight − 9 > Jennifer's weight − 9
Or suppose 8 > 3, then 8 − 2 > 3 − 2
Multiplication property:
z > 0
If x < y, and z > 0 then x × z < y × z
Example: Suppose 2 < 5, then 2 × 10 < 5 × 10 ( Notice that z = 10 and 10 > 0)
If x > y, and z > 0 then x × z > y × z
Example: Suppose 20 > 10, then 20 × 2 > 10 × 2
z < 0
If x < y, and z < 0 then x × z > y × z
Example: Suppose 2 < 5, then 2 × -4 > 5 × -4 ( -8 > -20. z = -4 and -4 < 0 )
If x > y, and z < 0 then x × z < y × z
Example: Suppose 5 > 1, then 5 × -2 < 1 × -2 ( -10 < -2 )
Division property:
It works exactly the same way as multiplication
z > 0
If x < y, and z > 0 then x ÷ z < y ÷ z
Example: Suppose 2 < 4, then 2 ÷ 2 < 4 ÷ 2
If x > y, and z > 0 then x ÷ z > y ÷ z
Example: Suppose 20 > 10, then 20 ÷ 5 > 10 ÷ 5
z < 0
If x < y, and z < 0 then x ÷ z > y ÷ z
Example: Suppose 4 < 8, then 4 ÷ -2 > 8 ÷ -2 ( -2 > -4 )
If x > y, and z < 0 then x ÷ z < y ÷ z
Example: Suppose 5 > 1, then 5 ÷ -1 < 1 ÷ -1 ( -5 < -1 )
Transitive property:
If x > y and y > z, then x > z
Example: Suppose 10 > 5 and 5 > 2, then 10 > 2
x < y and y < z, then x < z
5 < 10 and 10 < 20, then 5 < 20
Comparison property:
If x = y + z and z > 0 then x > y
Example: 6 = 4 + 2, then 6 > 4
The properties of inequality are more complicated to understand than the property of equality.
Allow yourself plenty of time as you go over this lesson.Any questions about the properties of inequality, let me know.