Prove that the Diagonals of a Kite are Perpendicular
Here in this lesson we will show how to prove that the diagonals of a kite are perpendicular using the kite shown below.
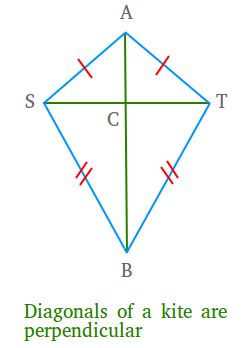
A theorem we need to prove that the diagonals of a kite are perpendicular
Converse of the perpendicular bisector theorem
If a point is equidistant from the endpoints of a line segment, then the point is on the perpendicular bisector of the segment.
Kite ATBS with AS ≅ AT and BS ≅ BT
Prove:
AB ⟂ ST
Since AS ≅ AT, A is equidistant from the endpoints S and T.
By the converse of the perpendicular bisector theorem, A lies on the perpendicular bisector of segment ST or ST.
Since BS ≅ BT, B is equidistant from the endpoints S and T.
By the converse of the perpendicular bisector theorem, B lies on the perpendicular bisector of segment ST or ST.
Therefore, both point A and point B lie on the perpendicular bisector of segment ST or ST.
Since there is exactly one line through any two points, AB must be the perpendicular bisector of ST
We can conclude that AB ⟂ ST