Converting from radians to degrees
To convert from radians to degrees, just multiply by (180 degrees) / (π radians). Let us briefly see why all we need to do is to multiply by (180 degrees) / (π radians).
Recall that the circumference of a circle is 2πr. Therefore, there are 2π radians in any circle.
2π radians is equivalent to 360 degrees or 2π radians = 360 degrees.
Divide both sides of 2π radians = 360 degrees by 2.
2π radians / 2 = 360 degrees / 2
π radians = 180 degrees
Now divide both sides of π radians = 180 degrees by π radians.
π radians / π radians = 180 degrees / π radians
1 = 180 degrees / π radians
1 radian = 180 degrees / π radians
Since 1 radian is equal to 180 degrees / π radians, we can just multiply any amount greater than 1 radian by 180 degrees / π radians to get the answer in degrees.
A few examples showing how to convert radians to degrees
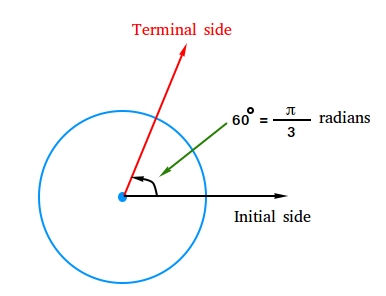
Example #1: Convert (π/3) radians to degrees
(π / 3) radians = (π radians / 3) × 180 degrees / π radians
= (π radians × 180 degrees) / 3 × π radians
= 180 degrees / 3
= 60 degrees
Notice that since π radians is on top and at the bottom, we can cancel it.
The figure above shows 60 degrees or π/3 radians.
If you were converting (-π/3) radians to degrees, the answer would be -60 degrees.
Example #2: Convert (π/2) radians to degrees
(π / 2) radians = (π radians / 2) × 180 degrees / π radians
= (π radians × 180 degrees) / 2 × π radians
= 180 degrees / 2
= 90 degrees
If you were converting (-π/2) radians to degrees, the answer would be -90 degrees.
Example #3: Convert (-π) radians to degrees
First, notice that (-π) radians = (-π / 1) radians
(-π / 1) radians = (-π radians / 1) × 180 degrees / π radians
= (-π radians × 180 degrees) / 1 × π radians
= -180 degrees / 1
= -180 degrees
Example #4: Convert (3π/4) radians to degrees
(3π / 4) radians = (3π radians / 4) × 180 degrees / π radians
= (3π radians × 180 degrees) / 4 × π radians
= (540 degrees × π radians) / 4 × π radians
= 540 degrees / 4
= 135 degrees