What is a radical expression?

A radical expression is a numerical expression or an algebraic expression that include a radical.

See below 2 examples of radical expressions.

Notice also that radical expressions can also have fractions as expressions.

There are 3 important pieces of information in any radical expressions that are important to identify. These are the radical sign, the radicand, and the index.

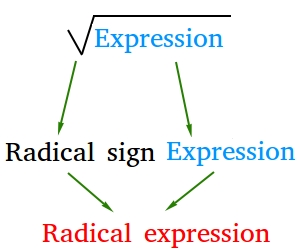
Take a look at the following radical expression.

• The symbol √ is called a radical sign

• The numerical expression or algebraic expression within the radical sign is called a radicand. In this case, the radicand is 32.

• The number 5 is called the index.

More information about a radical expression and its index

What if the index is n? Then the expression below means that we are looking for the nth root.

If the index n is even, the radicand a must be nonnegative for the root to be a real number. 

For example, the following radical expressions do not have a real number root because the indices are 4 and 2 and these are even numbers.

If the index n is an odd number, then the radicand do not have to be nonnegative for the root to be a real number. 

For example, the following radical expressions still have a real number root since the indices 3 and 5 are odd numbers.

More examples of radical expressions

The following radical expressions have algebraic expressions as radicands.

The following radical expressions have numerical expressions as radicands.

We can add, subtract, multiply, and divide radical expressions.