Range of a function

The range of a function is the set of all possible outputs of the function. When looking for the range, it may help to make a list of some ordered pairs for the function.

Example #1

What is the range of f(x) =  x² ?  

Pick { -4, -3, -2, -1, 0, 1, 2, 3, 4 } as your domain. The ordered pairs are

(-4, 16 ), (-3, 9),  (-2, 4), (-1, 1), (0, 0), (1, 1 ), (2, 4),  (3, 9), (4 , 16)

Range = {0, 1, 4, 9, 16} 

Notice that whether the number in the domain is positive or negative, the number in the range will always be positive.

Since f(x) represents the range values, the range is f(x) ≥ 0

Example #2: Trick when looking for the range of a function

What is the range of f(x) = x² + 3 ?

All we are doing here is adding 3 to the function of example #1. The only thing you need to notice is that when x = 0, f(0) = 3. So unlike the first example, the range does not start at 0 but at 3. For any other numbers in the domain, the numbers in the range will be positive and bigger than 3.

Therefore, range is f(x) ≥ 3. The range of x² + 3 is shown below.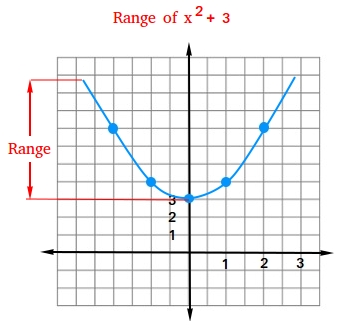

Example #3: Another trick when looking for the range of a function

What is the range of f(x) = x² - 3 ?

This is the same as example #2, except that we start at -3 instead of 3

Range is f(x) ≥ -3

Example #4 

What is the range of f(x) = x ?

The domain can be any real numbers. Since the numbers in the range are equal to the numbers in the domain, the range can be any real numbers as well.

More problems about range of function

Example #5

What is the range of f(x) = x³  ?

Pick { -4, -3, -2, -1, 0, 1, 2, 3, 4 } as your domain. The ordered pairs are

(-4, -64 ), (-3, -27),  (-2, -8), (-1, -1), (0, 0), (1, 1 ), (2, 8),  (3, 27), (4 , 64)

Range = {-64, -27, -8, -1, 0, 1, 8, 27, 64} 

Notice that when the numbers in the domain are positive, the numbers in the range are positive. Moreover, when the numbers in the domain are negative, the numbers in the range are negative as well. 

The range is f(x) ≥ 0 or f(x) < 0.

We can also write (-∞, ∞)

Example #6

What is the range of f(x) = √(x)?

Just notice that the numbers in the domain cannot be negative since we cannot take the square root of a negative number. The square root of a negative number has no answer with real numbers.

As a result, the numbers in the range will always be bigger or equal to zero. The range is f(x) ≥ 0

We can also write [0, ∞)

Example #7 is a tricky range of a function problem!

Example #7

What is the range of f(x) = 1/ x  ?

Notice that we can choose any number in the domain except 0

However, we can pick any number as close as possible to 0, or the number can be very big.

Suppose the numbers in the domain are positive. What happens when the numbers in the domain are closer and closer to 0 such as when x =  0.00001 or x = 0.0000001?

1 / 0.00001  = 100,000

1 / 0.0000001 = 10,000,000

The numbers in the range will get bigger and bigger.

What happens when the numbers in the domain are very big such as 100,000 or 100,000,000?

1 / 100000 = 0.00001

1 / 100,000,000 = 0.00000001

The numbers in the range will get smaller and smaller, but they will never be zero.

So far, when the domain is positive, the range is f(x) > 0

Similar logic can be used when the numbers in the domain are negative. When x is closer and closer to 0 such as when x  =  -0.00001 or  x = -0.0000001?

We get

1 / -0.00001  = -100,000

1 / -0.0000001 = -10,000,000

On the other hand when x is farther and farther away from 0 such as when x  = -100,000 or x = -100,000,000?

1 / -100000 = -0.00001

1 / -100,000,000 = -0.00000001

The range will be negative or f(x) < 0

Putting it together, range is (-∞ 0) U (0,-∞)