Solutions of systems with three variables

There 3 types of solutions of systems with three variables. A system can have 1 solution, infinitely many solutions, or no solutions. You can use graphs in three dimensions to represent systems of equations with three variables.

The solutions of a system of equations with three variables can be shown graphically as the intersections of planes.

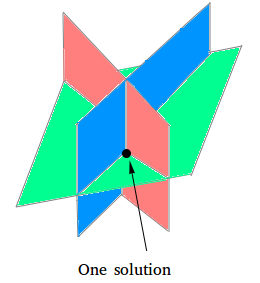
Systems with three variables with one solution

When a system with three variables has only one solution, the planes intersect at one common point.  The common point is shown in black in the figure below.

Systems with three variables with an infinite number of solutions

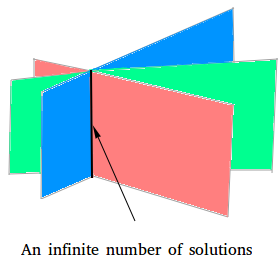
When a system with three variables has an infinite number of solutions, the planes intersect at all the points along a common line. The common line is shown in black above.

Systems with three variables with no solution

When systems with three variables have no solution, we call these systems inconsistent systems. A couple of cases could present itself. 

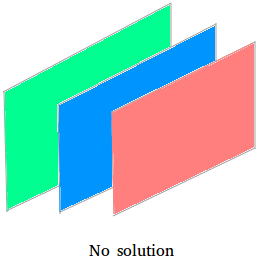
Case #1:

The three planes are parallel, so they never intersect.

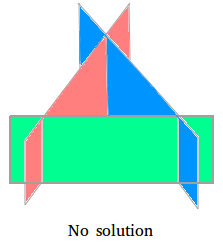
Case #2:

The planes intersect with each other. However, they do not intersect at a common point.