How to solve rational inequalities
The strategy that we will use to solve rational inequalities is by graphing the solution on the number line. It is much easier and more straightforward than other methods you may have seen online in my opinion. Let us start with an easy example and then we will move on to more complicated examples.
Example #1:
The rational expression has to be smaller than zero or negative. This can happen in the following two cases:
- The numerator (x + 3) is positive and the denominator (x - 4) is negative
- The numerator (x + 3) is negative and the denominator (x - 4) is positive.
Case #1:
x + 3 is positive or x + 3 > 0
x - 4 is negative or x - 4 < 0.
Just solve the two inequalities above.
x + 3 > 0
x + 3 - 3 > 0 - 3
x > -3
x - 4 < 0
x - 4 + 4 < 0 + 4
x < 4
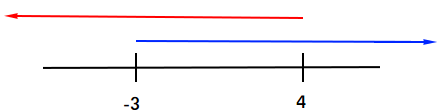
Graph x > -3 and x < 4
x > -3 is shown in blue and x < 4 is shown in red. The space where you see both red and blue at the same time is the solution.
The solution is any number between -3 and 4 or (-3, 4)
Case #2:
x + 3 is negative or x + 3 < 0
x - 4 is positive or x - 4 > 0.
Just solve the two inequalities above.
x + 3 < 0
x + 3 - 3 < 0 - 3
x < -3
x - 4 > 0
x - 4 + 4 > 0 + 4
x > 4
Graph x < -3 and x > 4
x < -3 is shown in red and x > 4 is shown in blue. Notice though that this time you do not see both red and blue at the same time. There is no solution in this case.
The solution is therefore just (-3, 4)
Example #2:
Example #2 is almost the same as example #1. The only difference is that the rational expression is also equal to zero.
The rational expression is equal to zero when the numerator or x + 3 is equal to zero.
x + 3 = 0
x + 3 - 3 = 0 - 3
x = -3
We just need to incorporate -3 into the solution we found in example #1.
All we need to do is to write [-3, 4) instead of (-3, 4).
The bracket means that -3 is now part of the solution.
Example #3:
First, solve when the rational expression is bigger than zero.
The rational expression has to be bigger than zero or positive. This can happen in the following two cases:
- The numerator (x2 + 3x + 2) is positive and the denominator (x2 - 16) is positive.
- The numerator (x2 + 3x + 2) is negative and the denominator (x2 - 16) is negative.
Case #1:
(x2 + 3x + 2) > 0
(x2 - 16) > 0
Just solve the two inequalities above.
(x2 + 3x + 2) > 0
(x + 2)(x + 1) > 0
You need to find the zeros for the inequality and then choose random values before, between, and after the zeros in order to determine where (x + 2)(x + 1) is bigger than zero.
(x + 2)(x + 1) = 0 when x + 2 = 0 and x + 1 = 0
The zeros are x = -2 and x = -1.
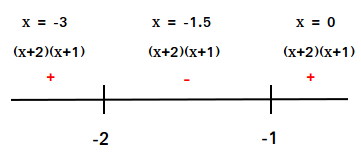Figure #3How did we determine the sign? For example, when x = 0, (0+2)(0+1) = (2)(1) = 2
Since 2 is positive, then (x + 2)(x + 1) is positive for any values you choose after -1.
Therefore, (x2 + 3x + 2) > 0 when x > -1 and x < -2
Now solve (x2 - 16) > 0
(x2 - 16) > 0
x2 - 16 + 16 > 0 + 16
x2 > 16
Take the square root of both sides
√(x2) > √(16)
|x| > 4
If x is positive, then |x| = x. So x > 4
If x is negative, then |x| = -x. So -x > 4
Multiply both sides of -x > 4 by -1.
x < -4
Therefore, x2 > 16 when x > 4 and x < -4
Summary
Graph x > -1, x < -2, x > 4, and x < -4
The space where you see both red and blue at the same time is the solution.
The solution is any number after 4 or any number before -4. We can write what we have so far as (4, ∞) or (-∞, -4)
Case #2:
(x2 + 3x + 2) < 0
(x2 - 16) < 0
Just solve the two inequalities above.
For (x2 + 3x + 2) < 0, we do not need to do any work since the answer is already in figure #3.
(x2 + 3x + 2) < 0 when x is between -2 and -1. This can also be written as x > - 2 and x < -1
Now solve (x2 - 16) < 0
(x2 - 16) < 0
x2 - 16 + 16 < 0 + 16
x2 < 16
Take the square root of both sides
√(x2) > √(16)
|x| < 4
If x is positive, then |x| = x. So x < 4
If x is negative, then |x| = -x. So -x < 4
Multiply both sides of -x < 4 by -1.
x > -4
Therefore, x2 < 16 when x < 4 and x > -4
Summary
Graph x > - 2, x < -1, x < 4 and x > -4
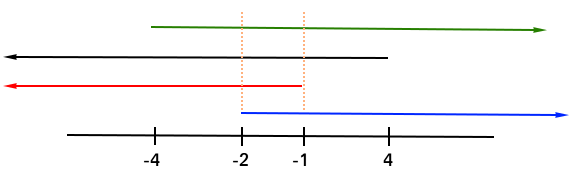
The space where you see red and blue, black, and green at the same time is the solution.
The solution is any number between -2 and -1. We can write what we have so far as (-2, -1)
Now, let us solve when the rational expression is equal to zero.
The rational expression is equal to zero when the numerator or x2 + 3x + 2 is equal to zero.
As already done, x2 + 3x + 2 = 0 when x = -2 or x = -1
We just need to incorporate -2 and -1 into the solution.
Final solution
In case #1, the solution is (4, ∞) or (-∞, -4)
In case #2, the solution is (-2, -1)
After incorporating -2 and -1 into the solution, the final solution is (4, ∞), (-∞, -4) , (-2, -1)