Standard normal distribution

The standard normal distribution (SND) is a special case of the normal distribution. When a normally distributed variable has a mean of 0 and a standard deviation of 1, we call this distribution standard normal distribution.

The random variable is denoted by z. In other words, notice that we use z instead of x to represent the units for the SND. The units for the SND are called z values, z scores, standard units, or standard scores.

A z score of 2 is a point that has a value of z = 2 and it is two standard deviations to the right of the mean.

A z score of -1 is a point that has a value of z = -1 and it is one standard deviation to the left of the mean.

As we saw in the lesson about normal distribution, the total area under the standard normal curve is equal to 1.

Also because of symmetry, the area on either side of the mean is 0.5.

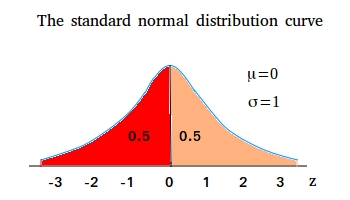
Notice that even though the z scores on the left of the mean are negative, the area under the curve is still positive.

Standard normal distribution word problems

Example #1:

Find the area under the standard normal curve between z = 0 and z = 1.84. To answer this question, you have to use the standard normal distribution table to locate the area.

First, divide the number 1.84 into 1.8 and 0.04 since 1.84 = 1.8 + 0.04.

To find the area, locate 1.8 in the column for z on the left side of the table and 0.04 in the row for z at the top of the table.

The entry where the row for 1.8 and the column for 0.04 intersect gives the area under the standard normal curve between z = 0 and z = 1.84.

After looking carefully in the table, this entry is 0.4671.

Example #2:

Find the area under the standard normal curve to the right of z = 3.02. To answer this question, you have to use again the standard normal distribution table to locate the area.

First, we need to find the area between z = 0 and z = 3.02. Then, we can subtract this area from 0.5, which is the total area to the right of z = 0.

Using a procedure similar to what you did in example #1, the area between z = 0 and z = 3.02 is 0.4987.

Therefore, the area under the standard normal curve to the right of z = 3.02 is 0.5 - 0.4987 = 0.0013.

Useful tips when looking for the area under the standard normal curve

• The area from z  = -2.14 to z  = 0 is the same as the area from z = 0 to z = 2.14 since the normal distribution is symmetric about the mean.

• The area to the right of z = -2.14 is equal to the area from z  = -2.14 to z  = 0 plus 0.5.