Subtraction in base two

Subtraction in base two is similar to subtracting numbers in base ten. If you do not quickly understand the examples below, do not worry, but keep reading.

Our goal with this lesson is to first help you understand deeply subtraction in base ten.

Then, as you learn how to subtract in base two, the similarity with base ten will allow you to grasp the concept better.

Base ten uses 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

How would you subtract 116 from 375 in base ten?

     3 7 5
   - 1 1 6
_____________


Since 5 is smaller than 6, you will borrow a ten from 7 tens.

7 tens is now 6 tens. Then, add the ten you borrowed to 5 to get 15.

Rewrite the problem as shown below.

          6  15
     3 7 5
   - 1 1 6
_____________


Base 2 uses only 0 and 1.

With base 2, you will borrow a 2,4,8,16, etc... depending on the place value, not a 10 when needed. Why is that?

Some explanations:

In base 10, the number 739 can mean everything you see below:

7 × 10² + 3 × 10 + 9

7 groups of 100, 3 groups of 10, and 9

7 hundreds + 3 tens + 9

In base 2, the number 101₂ could also mean everything you see below:

1 × 2² + 0 × 2 + 1

1 groups of 4, 0 groups of 2, and 1

1 four + 0 two + 1

Simply put, it is because you are in base 2, so any borrowing is done with 2, 4, 8, etc...

Say you want to perform the following subtraction in base two.

     1 1 0
   - 1 0 1
_____________


From the twos place, borrow 2 from 1 two. 1 two in now 0 two.

Then, add that 1 two to the 0 in the ones place to make it 1 two or 2.

Rewrite the problem and subtract.

          0   2
     1 1 0
   - 1 0 1
_____________
     0 0 1


Now you are ready to do some more subtraction in base two.

Example #2: No carry

To avoid confusion with base 10, we put a 2 next to each number.

However, if it is clear to you that the subtraction is being done in base two, there is no need to write down the 2.

     1 1 1₂
   - 0 1 0₂
_____________________
      1 0 1₂


The subtraction above is easy since there was no carry.

Subtraction in base two with carry

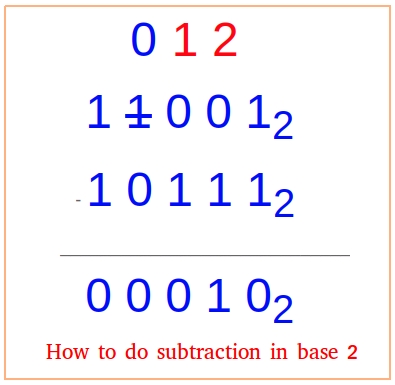
Read example #2 to see a detailed explanation of the subtraction in base two shown in the figure above.

Example #2

     1 1 0 0 1₂
   - 1 0 1 1 1₂
_________________________________
     1 1 0 0 0₂


Explanation:

Subtract the numbers in the ones place: 1 - 0 = 0

Write 0 in the ones place.

Now, you have a problem. You cannot subtract the numbers in the twos place, neither the numbers in the fours place.

You need to borrow 1 eight from the eights place. 1 eight is now 0 eight in that place.

However, 1 eight = 1 four + 2 twos.

Add 1 four to 0 four in the fours place to make it 1 four.

Add 2 twos to 0 two in the twos place to make it 2 twos.

Rewrite the problem and finish the subtraction.

              0   1 2
     1 1 0 0 1₂
   - 1 0 1 1 1₂
_________________________________
     0 0 0 1 0₂